A machine learning based algorithm selection method to solve the minimum cost flow problem
Paper and Code
Oct 03, 2022
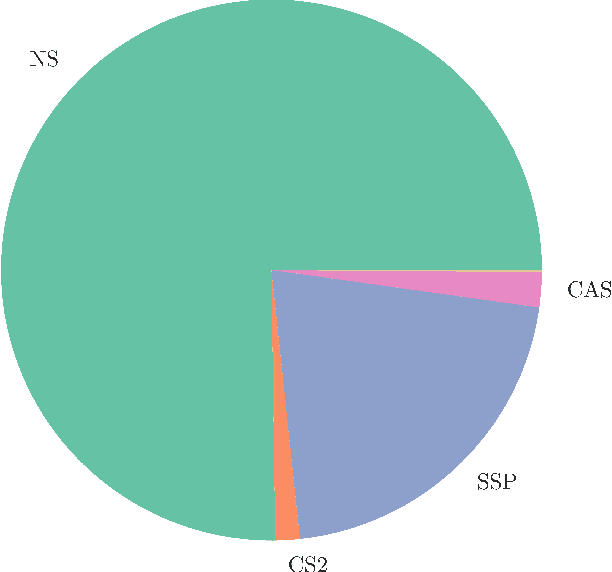
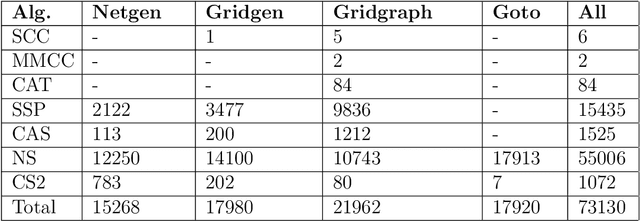
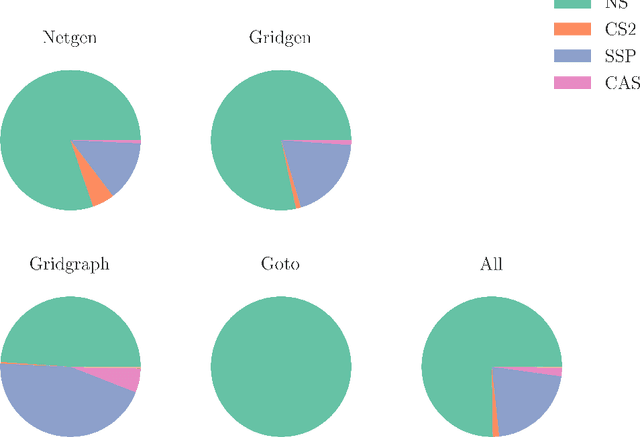
The minimum cost flow problem is one of the most studied network optimization problems and appears in numerous applications. Some efficient algorithms exist for this problem, which are freely available in the form of libraries or software packages. It is noticeable that none of these solvers is better than the other solution methods on all instances. Thus, the question arises whether the fastest algorithm can be selected for a given instance based on the characteristics of the instance. To this end, we train several machine learning classifiers to predict the fastest among a given set of solvers. We accomplish this by creating a representative data set of 81,000 instances and characterizing each of these instances by a vector of relevant features. To achieve better performance, we conduct a grid search to optimize the hyperparameters of the classifiers. Finally, we evaluate the different classifiers by means of accuracy. It is shown that tree-based models appear to adapt and exploit the relevant structures of the minimum-cost flow problem particularly well on a large number of instances, predicting the fastest solver with an accuracy of more than 90%.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge