DPRM: A Dual Implicit Process Reward Model in Multi-Hop Question Answering

In multi-hop question answering (MHQA) tasks, Chain of Thought (CoT) improves the quality of generation by guiding large language models (LLMs) through multi-step reasoning, and Knowledge Graphs (KGs) reduce hallucinations via semantic matching. Outcome Reward Models (ORMs) provide feedback after generating the final answers but fail to evaluate the process for multi-step reasoning. Traditional Process Reward Models (PRMs) evaluate the reasoning process but require costly human annotations or rollout generation. While implicit PRM is trained only with outcome signals and derives step rewards through reward parameterization without explicit annotations, it is more suitable for multi-step reasoning in MHQA tasks. However, existing implicit PRM has only been explored for plain text scenarios. When adapting to MHQA tasks, it cannot handle the graph structure constraints in KGs and capture the potential inconsistency between CoT and KG paths. To address these limitations, we propose the DPRM (Dual Implicit Process Reward Model). It trains two implicit PRMs for CoT and KG reasoning in MHQA tasks. Both PRMs, namely KG-PRM and CoT-PRM, derive step-level rewards from outcome signals via reward parameterization without additional explicit annotations. Among them, KG-PRM uses preference pairs to learn structural constraints from KGs. DPRM further introduces a consistency constraint between CoT and KG reasoning steps, making the two PRMs mutually verify and collaboratively optimize the reasoning paths. We also provide a theoretical demonstration of the derivation of process rewards. Experimental results show that our method outperforms 13 baselines on multiple datasets with up to 16.6% improvement on Hit@1.

Adversarial Graph Fusion for Incomplete Multi-view Semi-supervised Learning with Tensorial Imputation

View missing remains a significant challenge in graph-based multi-view semi-supervised learning, hindering their real-world applications. To address this issue, traditional methods introduce a missing indicator matrix and focus on mining partial structure among existing samples in each view for label propagation (LP). However, we argue that these disregarded missing samples sometimes induce discontinuous local structures, i.e., sub-clusters, breaking the fundamental smoothness assumption in LP. Consequently, such a Sub-Cluster Problem (SCP) would distort graph fusion and degrade classification performance. To alleviate SCP, we propose a novel incomplete multi-view semi-supervised learning method, termed AGF-TI. Firstly, we design an adversarial graph fusion scheme to learn a robust consensus graph against the distorted local structure through a min-max framework. By stacking all similarity matrices into a tensor, we further recover the incomplete structure from the high-order consistency information based on the low-rank tensor learning. Additionally, the anchor-based strategy is incorporated to reduce the computational complexity. An efficient alternative optimization algorithm combining a reduced gradient descent method is developed to solve the formulated objective, with theoretical convergence. Extensive experimental results on various datasets validate the superiority of our proposed AGF-TI as compared to state-of-the-art methods. Code is available at https://github.com/ZhangqiJiang07/AGF_TI.

Devils in Middle Layers of Large Vision-Language Models: Interpreting, Detecting and Mitigating Object Hallucinations via Attention Lens

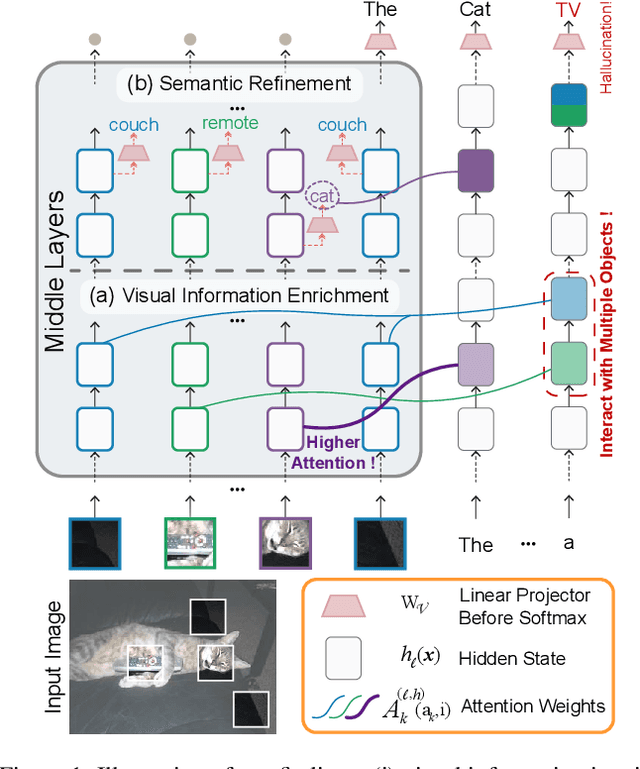
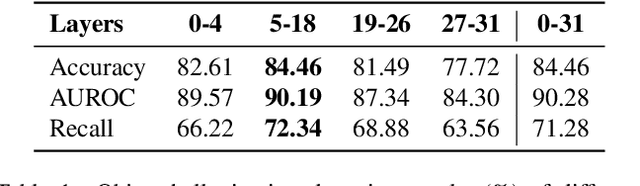
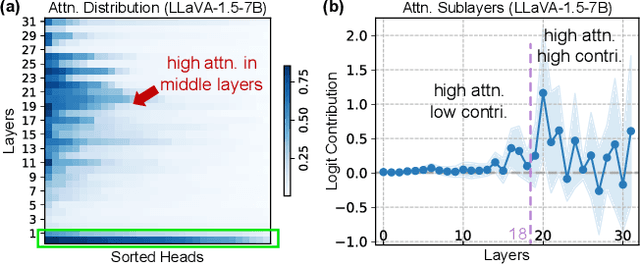
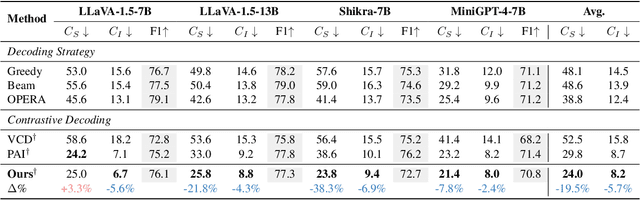
Hallucinations in Large Vision-Language Models (LVLMs) significantly undermine their reliability, motivating researchers to explore the causes of hallucination. However, most studies primarily focus on the language aspect rather than the visual. In this paper, we address how LVLMs process visual information and whether this process causes hallucination. Firstly, we use the attention lens to identify the stages at which LVLMs handle visual data, discovering that the middle layers are crucial. Moreover, we find that these layers can be further divided into two stages: "visual information enrichment" and "semantic refinement" which respectively propagate visual data to object tokens and interpret it through text. By analyzing attention patterns during the visual information enrichment stage, we find that real tokens consistently receive higher attention weights than hallucinated ones, serving as a strong indicator of hallucination. Further examination of multi-head attention maps reveals that hallucination tokens often result from heads interacting with inconsistent objects. Based on these insights, we propose a simple inference-time method that adjusts visual attention by integrating information across various heads. Extensive experiments demonstrate that this approach effectively mitigates hallucinations in mainstream LVLMs without additional training costs.

Nonconvex One-bit Single-label Multi-label Learning

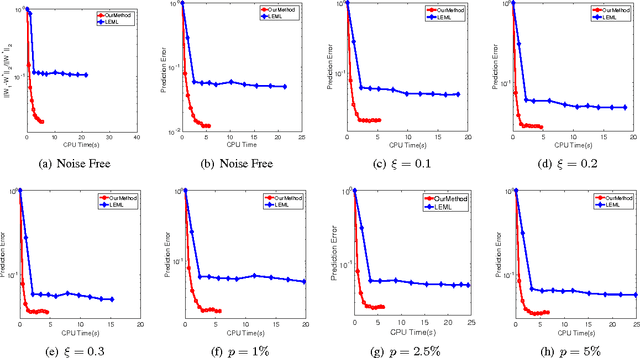
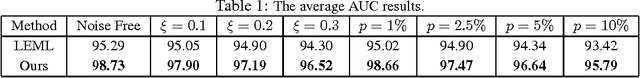
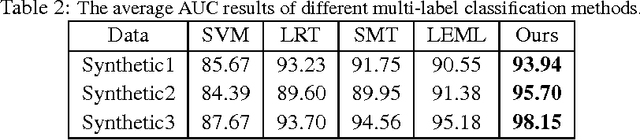
We study an extreme scenario in multi-label learning where each training instance is endowed with a single one-bit label out of multiple labels. We formulate this problem as a non-trivial special case of one-bit rank-one matrix sensing and develop an efficient non-convex algorithm based on alternating power iteration. The proposed algorithm is able to recover the underlying low-rank matrix model with linear convergence. For a rank-$k$ model with $d_1$ features and $d_2$ classes, the proposed algorithm achieves $O(\epsilon)$ recovery error after retrieving $O(k^{1.5}d_1 d_2/\epsilon)$ one-bit labels within $O(kd)$ memory. Our bound is nearly optimal in the order of $O(1/\epsilon)$. This significantly improves the state-of-the-art sampling complexity of one-bit multi-label learning. We perform experiments to verify our theory and evaluate the performance of the proposed algorithm.