Nonconvex One-bit Single-label Multi-label Learning
Paper and Code
Mar 17, 2017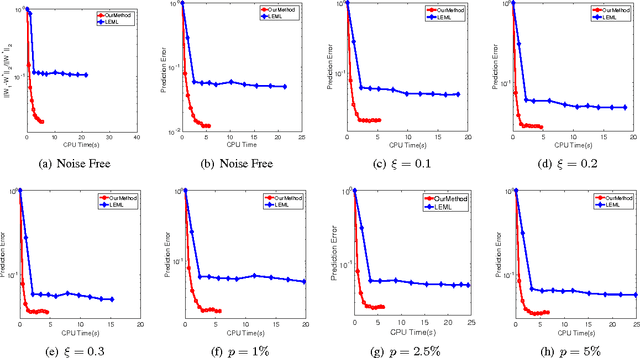
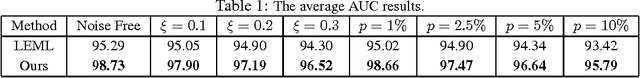
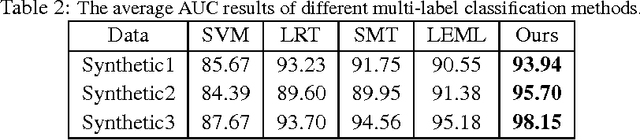
We study an extreme scenario in multi-label learning where each training instance is endowed with a single one-bit label out of multiple labels. We formulate this problem as a non-trivial special case of one-bit rank-one matrix sensing and develop an efficient non-convex algorithm based on alternating power iteration. The proposed algorithm is able to recover the underlying low-rank matrix model with linear convergence. For a rank-$k$ model with $d_1$ features and $d_2$ classes, the proposed algorithm achieves $O(\epsilon)$ recovery error after retrieving $O(k^{1.5}d_1 d_2/\epsilon)$ one-bit labels within $O(kd)$ memory. Our bound is nearly optimal in the order of $O(1/\epsilon)$. This significantly improves the state-of-the-art sampling complexity of one-bit multi-label learning. We perform experiments to verify our theory and evaluate the performance of the proposed algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge