SAGEval: The frontiers of Satisfactory Agent based NLG Evaluation for reference-free open-ended text

Large Language Model (LLM) integrations into applications like Microsoft365 suite and Google Workspace for creating/processing documents, emails, presentations, etc. has led to considerable enhancements in productivity and time savings. But as these integrations become more more complex, it is paramount to ensure that the quality of output from the LLM-integrated applications are relevant and appropriate for use. Identifying the need to develop robust evaluation approaches for natural language generation, wherein references/ground labels doesn't exist or isn't amply available, this paper introduces a novel framework called "SAGEval" which utilizes a critiquing Agent to provide feedback on scores generated by LLM evaluators. We show that the critiquing Agent is able to rectify scores from LLM evaluators, in absence of references/ground-truth labels, thereby reducing the need for labeled data even for complex NLG evaluation scenarios, like the generation of JSON-structured forms/surveys with responses in different styles like multiple choice, likert ratings, single choice questions, etc.

Gaussian Graphical Model Selection for Huge Data via Minipatch Learning

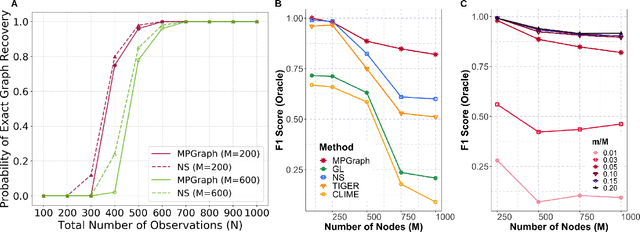
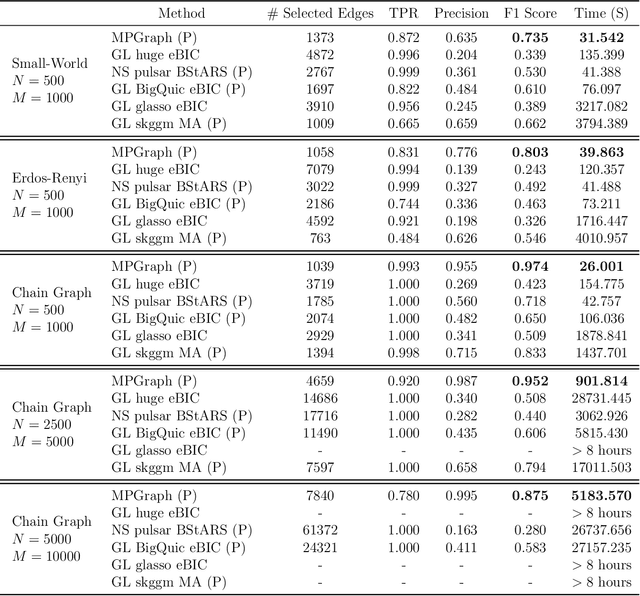
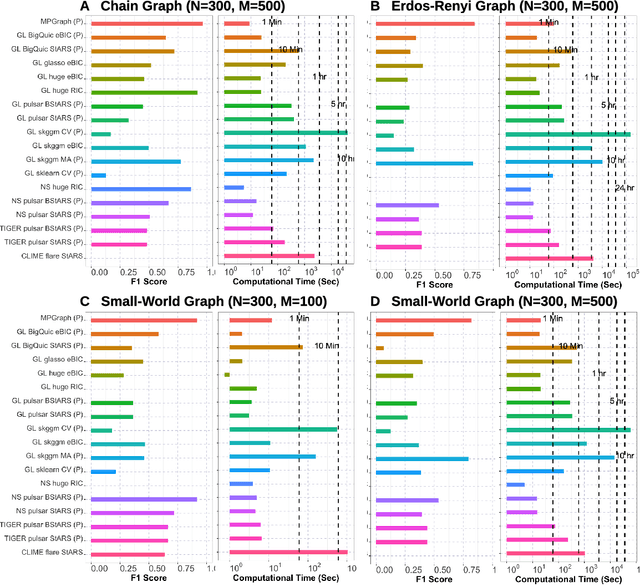
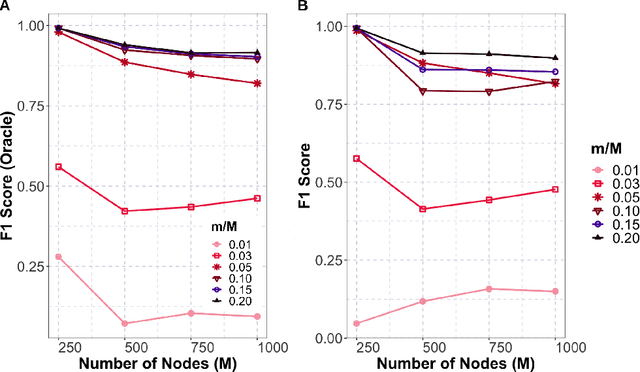
Gaussian graphical models are essential unsupervised learning techniques to estimate conditional dependence relationships between sets of nodes. While graphical model selection is a well-studied problem with many popular techniques, there are typically three key practical challenges: i) many existing methods become computationally intractable in huge-data settings with tens of thousands of nodes; ii) the need for separate data-driven tuning hyperparameter selection procedures considerably adds to the computational burden; iii) the statistical accuracy of selected edges often deteriorates as the dimension and/or the complexity of the underlying graph structures increase. We tackle these problems by proposing the Minipatch Graph (MPGraph) estimator. Our approach builds upon insights from the latent variable graphical model problem and utilizes ensembles of thresholded graph estimators fit to tiny, random subsets of both the observations and the nodes, termed minipatches. As estimates are fit on small problems, our approach is computationally fast with integrated stability-based hyperparameter tuning. Additionally, we prove that under certain conditions our MPGraph algorithm achieves finite-sample graph selection consistency. We compare our approach to state-of-the-art computational approaches to Gaussian graphical model selection including the BigQUIC algorithm, and empirically demonstrate that our approach is not only more accurate but also extensively faster for huge graph selection problems.

Feature Selection for Huge Data via Minipatch Learning

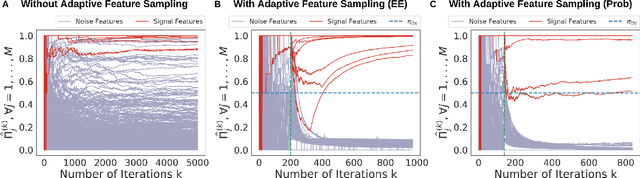
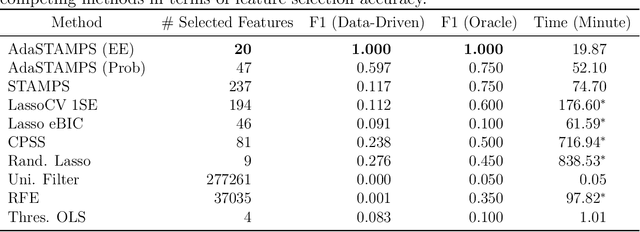
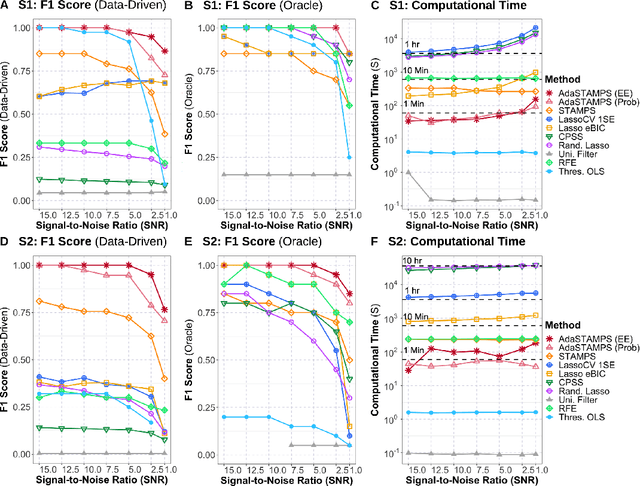
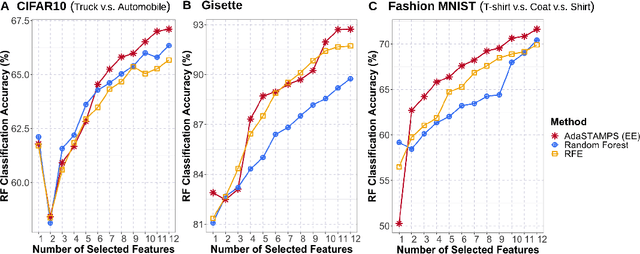
Feature selection often leads to increased model interpretability, faster computation, and improved model performance by discarding irrelevant or redundant features. While feature selection is a well-studied problem with many widely-used techniques, there are typically two key challenges: i) many existing approaches become computationally intractable in huge-data settings with millions of observations and features; and ii) the statistical accuracy of selected features degrades in high-noise, high-correlation settings, thus hindering reliable model interpretation. We tackle these problems by proposing Stable Minipatch Selection (STAMPS) and Adaptive STAMPS (AdaSTAMPS). These are meta-algorithms that build ensembles of selection events of base feature selectors trained on many tiny, (adaptively-chosen) random subsets of both the observations and features of the data, which we call minipatches. Our approaches are general and can be employed with a variety of existing feature selection strategies and machine learning techniques. In addition, we provide theoretical insights on STAMPS and empirically demonstrate that our approaches, especially AdaSTAMPS, dominate competing methods in terms of feature selection accuracy and computational time.

Supervised Convex Clustering

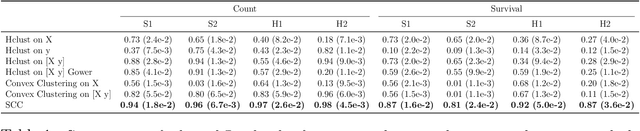
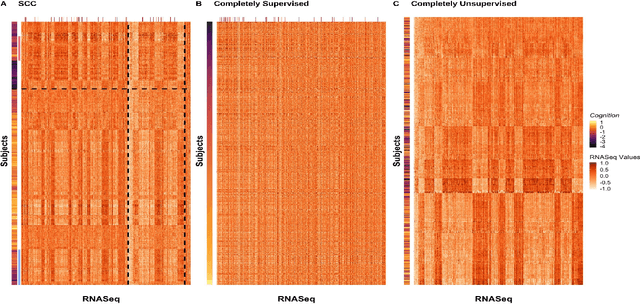
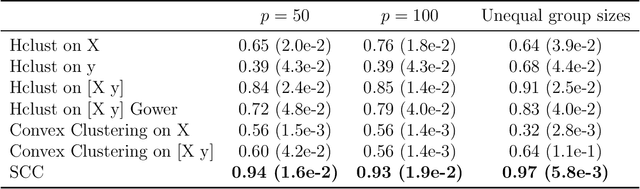
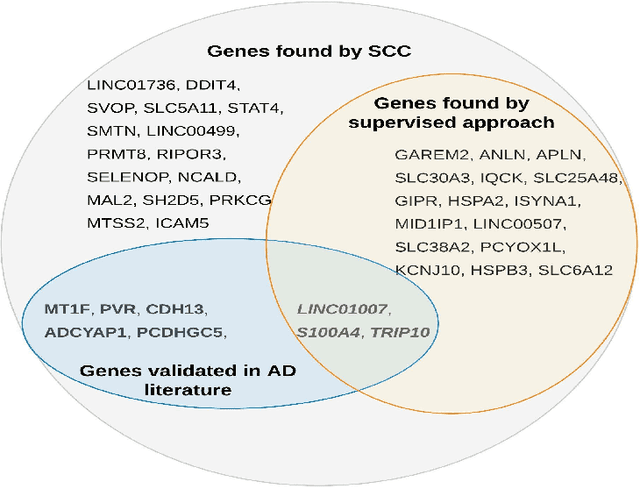
Clustering has long been a popular unsupervised learning approach to identify groups of similar objects and discover patterns from unlabeled data in many applications. Yet, coming up with meaningful interpretations of the estimated clusters has often been challenging precisely due to its unsupervised nature. Meanwhile, in many real-world scenarios, there are some noisy supervising auxiliary variables, for instance, subjective diagnostic opinions, that are related to the observed heterogeneity of the unlabeled data. By leveraging information from both supervising auxiliary variables and unlabeled data, we seek to uncover more scientifically interpretable group structures that may be hidden by completely unsupervised analyses. In this work, we propose and develop a new statistical pattern discovery method named Supervised Convex Clustering (SCC) that borrows strength from both information sources and guides towards finding more interpretable patterns via a joint convex fusion penalty. We develop several extensions of SCC to integrate different types of supervising auxiliary variables, to adjust for additional covariates, and to find biclusters. We demonstrate the practical advantages of SCC through simulations and a case study on Alzheimer's Disease genomics. Specifically, we discover new candidate genes as well as new subtypes of Alzheimer's Disease that can potentially lead to better understanding of the underlying genetic mechanisms responsible for the observed heterogeneity of cognitive decline in older adults.

Clustered Gaussian Graphical Model via Symmetric Convex Clustering

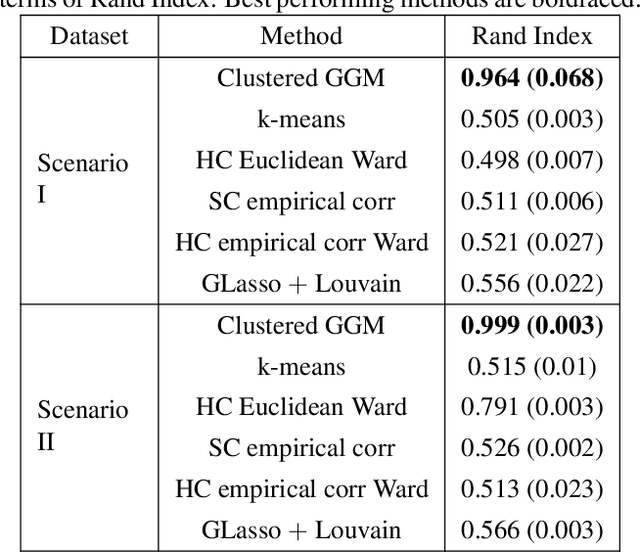
Knowledge of functional groupings of neurons can shed light on structures of neural circuits and is valuable in many types of neuroimaging studies. However, accurately determining which neurons carry out similar neurological tasks via controlled experiments is both labor-intensive and prohibitively expensive on a large scale. Thus, it is of great interest to cluster neurons that have similar connectivity profiles into functionally coherent groups in a data-driven manner. In this work, we propose the clustered Gaussian graphical model (GGM) and a novel symmetric convex clustering penalty in an unified convex optimization framework for inferring functional clusters among neurons from neural activity data. A parallelizable multi-block Alternating Direction Method of Multipliers (ADMM) algorithm is used to solve the corresponding convex optimization problem. In addition, we establish convergence guarantees for the proposed ADMM algorithm. Experimental results on both synthetic data and real-world neuroscientific data demonstrate the effectiveness of our approach.