Thomas Linsbichler
Solving Advanced Argumentation Problems with Answer Set Programming
Dec 05, 2019
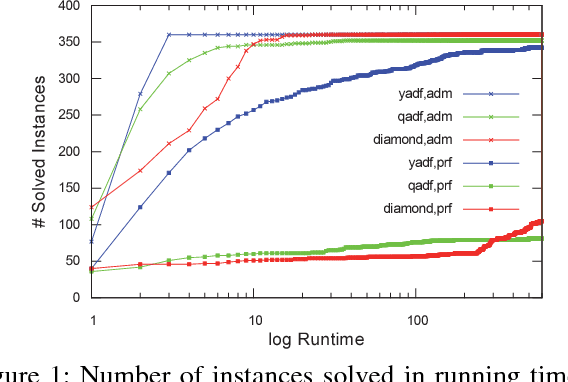
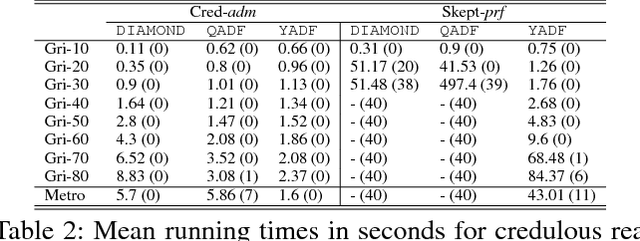
Abstract:Powerful formalisms for abstract argumentation have been proposed, among them abstract dialectical frameworks (ADFs) that allow for a succinct and flexible specification of the relationship between arguments, and the GRAPPA framework which allows argumentation scenarios to be represented as arbitrary edge-labelled graphs. The complexity of ADFs and GRAPPA is located beyond NP and ranges up to the third level of the polynomial hierarchy. The combined complexity of Answer Set Programming (ASP) exactly matches this complexity when programs are restricted to predicates of bounded arity. In this paper, we exploit this coincidence and present novel efficient translations from ADFs and GRAPPA to ASP. More specifically, we provide reductions for the five main ADF semantics of admissible, complete, preferred, grounded, and stable interpretations, and exemplify how these reductions need to be adapted for GRAPPA for the admissible, complete and preferred semantics. Under consideration in Theory and Practice of Logic Programming (TPLP).
Design and Results of the Second International Competition on Computational Models of Argumentation
Sep 02, 2019


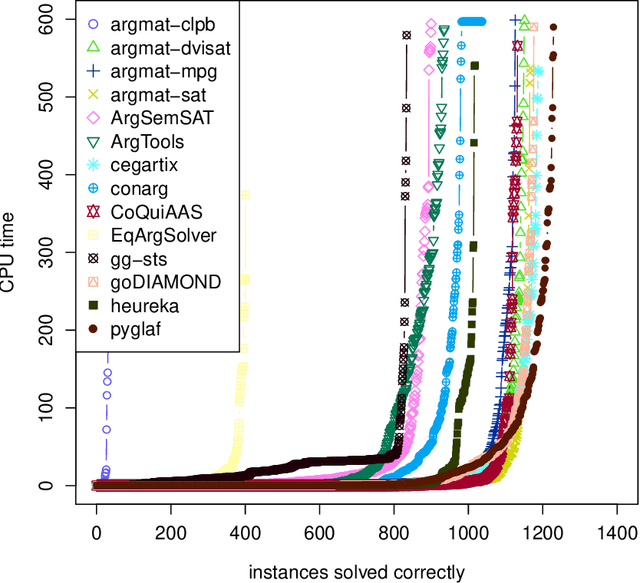
Abstract:Argumentation is a major topic in the study of Artificial Intelligence. Since the first edition in 2015, advancements in solving (abstract) argumentation frameworks are assessed in competition events, similar to other closely related problem solving technologies. In this paper, we report about the design and results of the Second International Competition on Computational Models of Argumentation, which has been jointly organized by TU Dresden (Germany), TU Wien (Austria), and the University of Genova (Italy), in affiliation with the 2017 International Workshop on Theory and Applications of Formal Argumentation. This second edition maintains some of the design choices made in the first event, e.g. the I/O formats, the basic reasoning problems, and the organization into tasks and tracks. At the same time, it introduces significant novelties, e.g. three additional prominent semantics, and an instance selection stage for classifying instances according to their empirical hardness.
Characterizing Realizability in Abstract Argumentation
Mar 31, 2016
Abstract:Realizability for knowledge representation formalisms studies the following question: given a semantics and a set of interpretations, is there a knowledge base whose semantics coincides exactly with the given interpretation set? We introduce a general framework for analyzing realizability in abstract dialectical frameworks (ADFs) and various of its subclasses. In particular, the framework applies to Dung argumentation frameworks, SETAFs by Nielsen and Parsons, and bipolar ADFs. We present a uniform characterization method for the admissible, complete, preferred and model/stable semantics. We employ this method to devise an algorithm that decides realizability for the mentioned formalisms and semantics; moreover the algorithm allows for constructing a desired knowledge base whenever one exists. The algorithm is built in a modular way and thus easily extensible to new formalisms and semantics. We have also implemented our approach in answer set programming, and used the implementation to obtain several novel results on the relative expressiveness of the abovementioned formalisms.
Verifiability of Argumentation Semantics
Mar 31, 2016
Abstract:Dung's abstract argumentation theory is a widely used formalism to model conflicting information and to draw conclusions in such situations. Hereby, the knowledge is represented by so-called argumentation frameworks (AFs) and the reasoning is done via semantics extracting acceptable sets. All reasonable semantics are based on the notion of conflict-freeness which means that arguments are only jointly acceptable when they are not linked within the AF. In this paper, we study the question which information on top of conflict-free sets is needed to compute extensions of a semantics at hand. We introduce a hierarchy of so-called verification classes specifying the required amount of information. We show that well-known standard semantics are exactly verifiable through a certain such class. Our framework also gives a means to study semantics lying inbetween known semantics, thus contributing to a more abstract understanding of the different features argumentation semantics offer.
Compact Argumentation Frameworks
Apr 30, 2014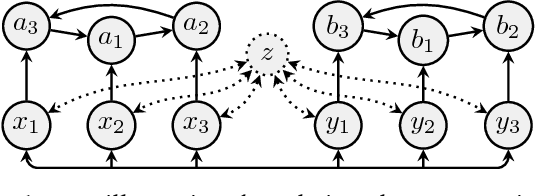
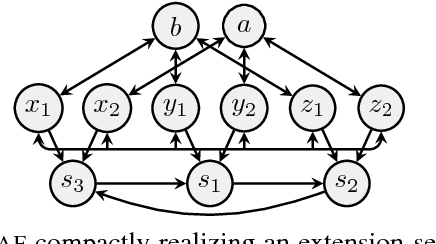


Abstract:Abstract argumentation frameworks (AFs) are one of the most studied formalisms in AI. In this work, we introduce a certain subclass of AFs which we call compact. Given an extension-based semantics, the corresponding compact AFs are characterized by the feature that each argument of the AF occurs in at least one extension. This not only guarantees a certain notion of fairness; compact AFs are thus also minimal in the sense that no argument can be removed without changing the outcome. We address the following questions in the paper: (1) How are the classes of compact AFs related for different semantics? (2) Under which circumstances can AFs be transformed into equivalent compact ones? (3) Finally, we show that compact AFs are indeed a non-trivial subclass, since the verification problem remains coNP-hard for certain semantics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge