Compact Argumentation Frameworks
Paper and Code
Apr 30, 2014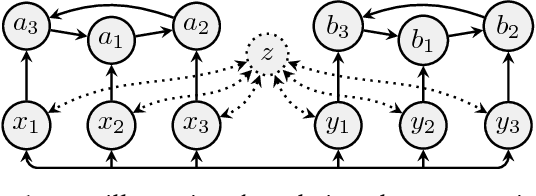
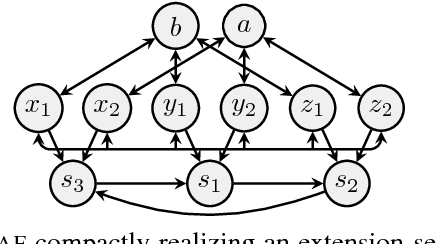


Abstract argumentation frameworks (AFs) are one of the most studied formalisms in AI. In this work, we introduce a certain subclass of AFs which we call compact. Given an extension-based semantics, the corresponding compact AFs are characterized by the feature that each argument of the AF occurs in at least one extension. This not only guarantees a certain notion of fairness; compact AFs are thus also minimal in the sense that no argument can be removed without changing the outcome. We address the following questions in the paper: (1) How are the classes of compact AFs related for different semantics? (2) Under which circumstances can AFs be transformed into equivalent compact ones? (3) Finally, we show that compact AFs are indeed a non-trivial subclass, since the verification problem remains coNP-hard for certain semantics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge