Ringo Baumann
On the Existence of Characterization Logics and Fundamental Properties of Argumentation Semantics
Mar 02, 2020



Abstract:Given the large variety of existing logical formalisms it is of utmost importance to select the most adequate one for a specific purpose, e.g. for representing the knowledge relevant for a particular application or for using the formalism as a modeling tool for problem solving. Awareness of the nature of a logical formalism, in other words, of its fundamental intrinsic properties, is indispensable and provides the basis of an informed choice. In this treatise we consider the existence characterization logics as well as properties like existence and uniqueness, expressibility, replaceability and verifiability in the realm of abstract argumentation
* Treatise
Verifiability of Argumentation Semantics
Mar 31, 2016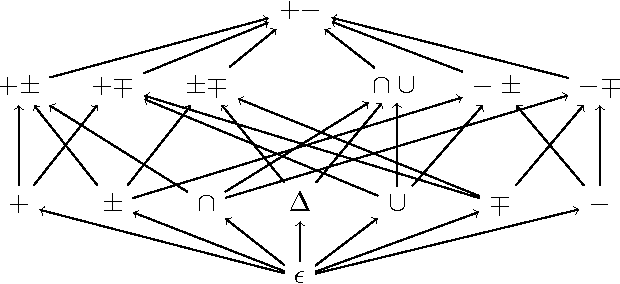
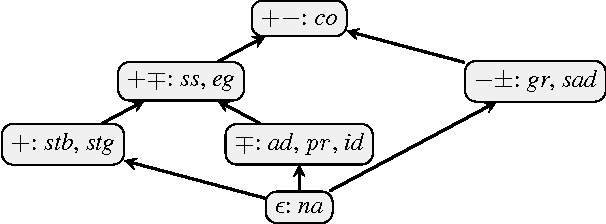
Abstract:Dung's abstract argumentation theory is a widely used formalism to model conflicting information and to draw conclusions in such situations. Hereby, the knowledge is represented by so-called argumentation frameworks (AFs) and the reasoning is done via semantics extracting acceptable sets. All reasonable semantics are based on the notion of conflict-freeness which means that arguments are only jointly acceptable when they are not linked within the AF. In this paper, we study the question which information on top of conflict-free sets is needed to compute extensions of a semantics at hand. We introduce a hierarchy of so-called verification classes specifying the required amount of information. We show that well-known standard semantics are exactly verifiable through a certain such class. Our framework also gives a means to study semantics lying inbetween known semantics, thus contributing to a more abstract understanding of the different features argumentation semantics offer.
Compact Argumentation Frameworks
Apr 30, 2014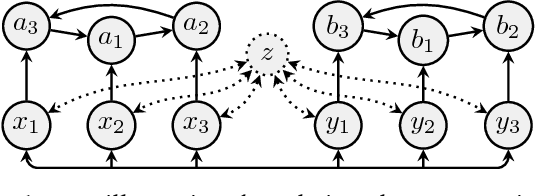
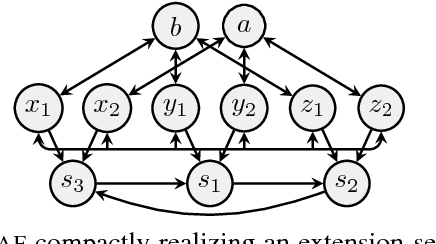


Abstract:Abstract argumentation frameworks (AFs) are one of the most studied formalisms in AI. In this work, we introduce a certain subclass of AFs which we call compact. Given an extension-based semantics, the corresponding compact AFs are characterized by the feature that each argument of the AF occurs in at least one extension. This not only guarantees a certain notion of fairness; compact AFs are thus also minimal in the sense that no argument can be removed without changing the outcome. We address the following questions in the paper: (1) How are the classes of compact AFs related for different semantics? (2) Under which circumstances can AFs be transformed into equivalent compact ones? (3) Finally, we show that compact AFs are indeed a non-trivial subclass, since the verification problem remains coNP-hard for certain semantics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge