Verifiability of Argumentation Semantics
Paper and Code
Mar 31, 2016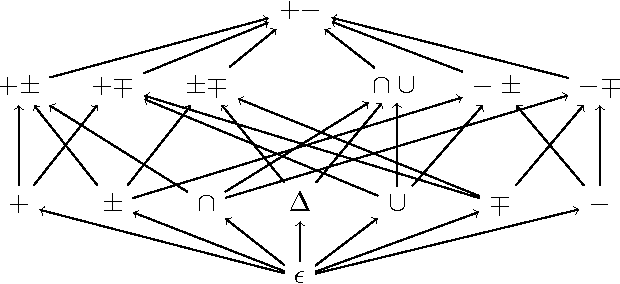
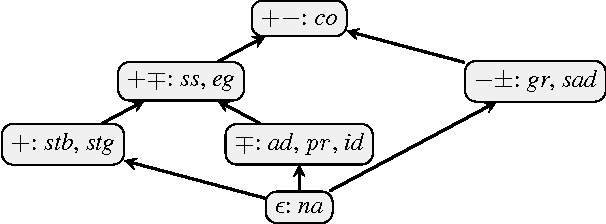
Dung's abstract argumentation theory is a widely used formalism to model conflicting information and to draw conclusions in such situations. Hereby, the knowledge is represented by so-called argumentation frameworks (AFs) and the reasoning is done via semantics extracting acceptable sets. All reasonable semantics are based on the notion of conflict-freeness which means that arguments are only jointly acceptable when they are not linked within the AF. In this paper, we study the question which information on top of conflict-free sets is needed to compute extensions of a semantics at hand. We introduce a hierarchy of so-called verification classes specifying the required amount of information. We show that well-known standard semantics are exactly verifiable through a certain such class. Our framework also gives a means to study semantics lying inbetween known semantics, thus contributing to a more abstract understanding of the different features argumentation semantics offer.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge