Solving Advanced Argumentation Problems with Answer Set Programming
Paper and Code
Dec 05, 2019
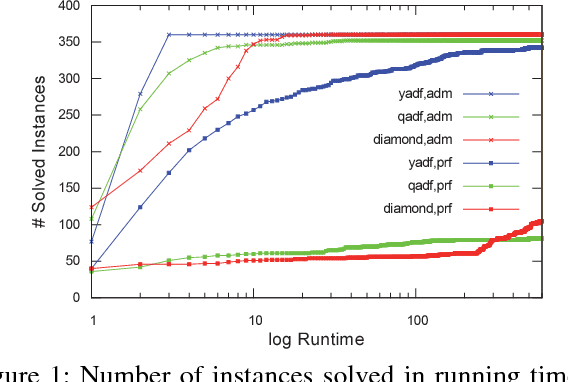
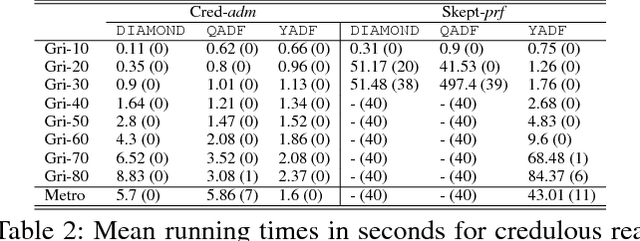
Powerful formalisms for abstract argumentation have been proposed, among them abstract dialectical frameworks (ADFs) that allow for a succinct and flexible specification of the relationship between arguments, and the GRAPPA framework which allows argumentation scenarios to be represented as arbitrary edge-labelled graphs. The complexity of ADFs and GRAPPA is located beyond NP and ranges up to the third level of the polynomial hierarchy. The combined complexity of Answer Set Programming (ASP) exactly matches this complexity when programs are restricted to predicates of bounded arity. In this paper, we exploit this coincidence and present novel efficient translations from ADFs and GRAPPA to ASP. More specifically, we provide reductions for the five main ADF semantics of admissible, complete, preferred, grounded, and stable interpretations, and exemplify how these reductions need to be adapted for GRAPPA for the admissible, complete and preferred semantics. Under consideration in Theory and Practice of Logic Programming (TPLP).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge