Gerhard Brewka
Solving Advanced Argumentation Problems with Answer Set Programming
Dec 05, 2019
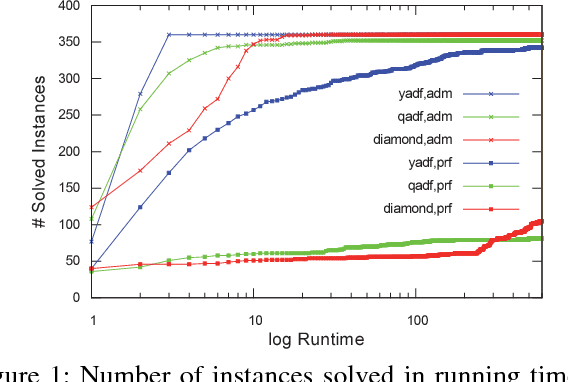
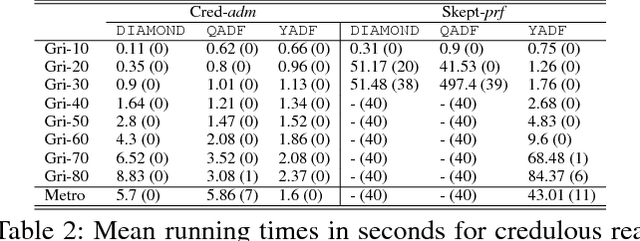
Abstract:Powerful formalisms for abstract argumentation have been proposed, among them abstract dialectical frameworks (ADFs) that allow for a succinct and flexible specification of the relationship between arguments, and the GRAPPA framework which allows argumentation scenarios to be represented as arbitrary edge-labelled graphs. The complexity of ADFs and GRAPPA is located beyond NP and ranges up to the third level of the polynomial hierarchy. The combined complexity of Answer Set Programming (ASP) exactly matches this complexity when programs are restricted to predicates of bounded arity. In this paper, we exploit this coincidence and present novel efficient translations from ADFs and GRAPPA to ASP. More specifically, we provide reductions for the five main ADF semantics of admissible, complete, preferred, grounded, and stable interpretations, and exemplify how these reductions need to be adapted for GRAPPA for the admissible, complete and preferred semantics. Under consideration in Theory and Practice of Logic Programming (TPLP).
Weighted Abstract Dialectical Frameworks: Extended and Revised Report
Sep 07, 2018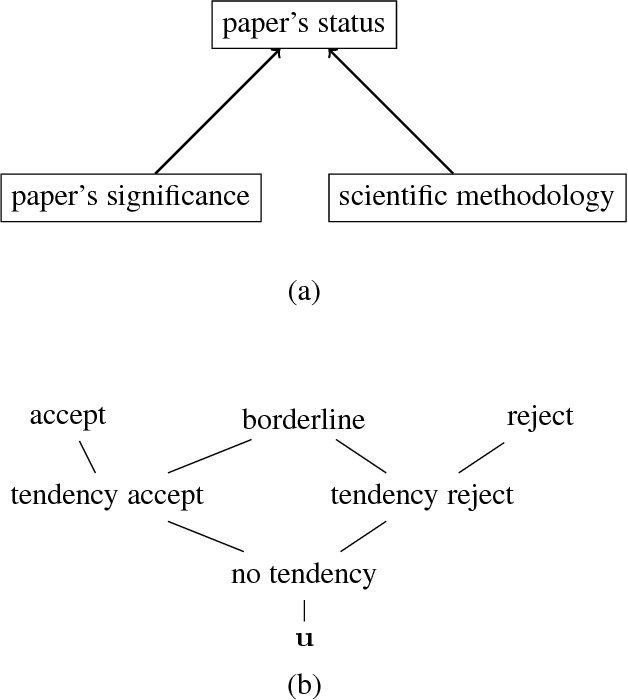
Abstract:Abstract Dialectical Frameworks (ADFs) generalize Dung's argumentation frameworks allowing various relationships among arguments to be expressed in a systematic way. We further generalize ADFs so as to accommodate arbitrary acceptance degrees for the arguments. This makes ADFs applicable in domains where both the initial status of arguments and their relationship are only insufficiently specified by Boolean functions. We define all standard ADF semantics for the weighted case, including grounded, preferred and stable semantics. We illustrate our approach using acceptance degrees from the unit interval and show how other valuation structures can be integrated. In each case it is sufficient to specify how the generalized acceptance conditions are represented by formulas, and to specify the information ordering underlying the characteristic ADF operator. We also present complexity results for problems related to weighted ADFs.
Reactive Multi-Context Systems: Heterogeneous Reasoning in Dynamic Environments
Dec 11, 2017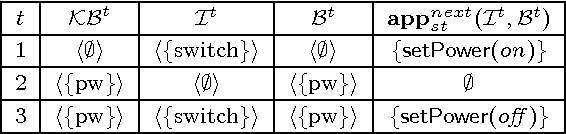
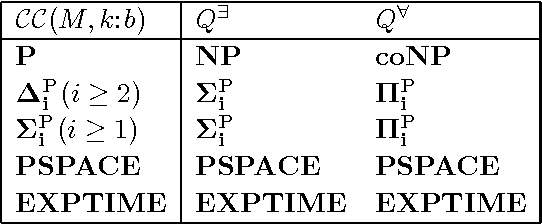

Abstract:Managed multi-context systems (mMCSs) allow for the integration of heterogeneous knowledge sources in a modular and very general way. They were, however, mainly designed for static scenarios and are therefore not well-suited for dynamic environments in which continuous reasoning over such heterogeneous knowledge with constantly arriving streams of data is necessary. In this paper, we introduce reactive multi-context systems (rMCSs), a framework for reactive reasoning in the presence of heterogeneous knowledge sources and data streams. We show that rMCSs are indeed well-suited for this purpose by illustrating how several typical problems arising in the context of stream reasoning can be handled using them, by showing how inconsistencies possibly occurring in the integration of multiple knowledge sources can be handled, and by arguing that the potential non-determinism of rMCSs can be avoided if needed using an alternative, more skeptical well-founded semantics instead with beneficial computational properties. We also investigate the computational complexity of various reasoning problems related to rMCSs. Finally, we discuss related work, and show that rMCSs do not only generalize mMCSs to dynamic settings, but also capture/extend relevant approaches w.r.t. dynamics in knowledge representation and stream reasoning.
Multi-Context Systems for Reactive Reasoning in Dynamic Environments
May 20, 2015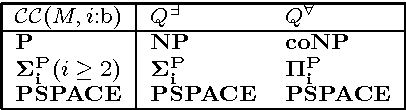
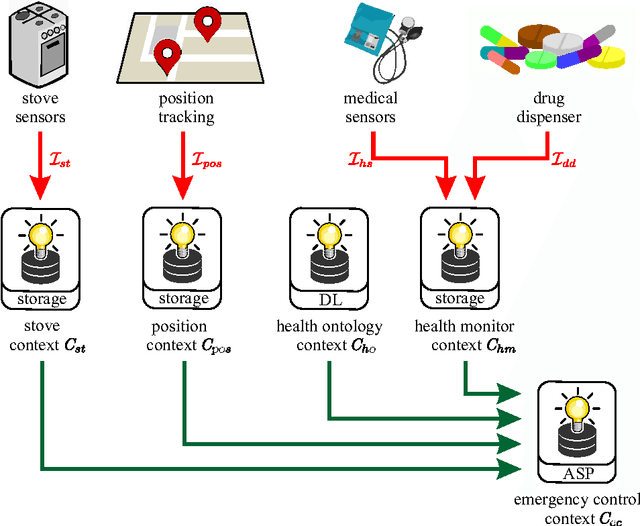
Abstract:We show in this paper how managed multi-context systems (mMCSs) can be turned into a reactive formalism suitable for continuous reasoning in dynamic environments. We extend mMCSs with (abstract) sensors and define the notion of a run of the extended systems. We then show how typical problems arising in online reasoning can be addressed: handling potentially inconsistent sensor input, modeling intelligent forms of forgetting, selective integration of knowledge, and controlling the reasoning effort spent by contexts, like setting contexts to an idle mode. We also investigate the complexity of some important related decision problems and discuss different design choices which are given to the knowledge engineer.
Logic Programming with Ordered Disjunction
Jul 11, 2002Abstract:Logic programs with ordered disjunction (LPODs) combine ideas underlying Qualitative Choice Logic (Brewka et al. KR 2002) and answer set programming. Logic programming under answer set semantics is extended with a new connective called ordered disjunction. The new connective allows us to represent alternative, ranked options for problem solutions in the heads of rules: A \times B intuitively means: if possible A, but if A is not possible then at least B. The semantics of logic programs with ordered disjunction is based on a preference relation on answer sets. LPODs are useful for applications in design and configuration and can serve as a basis for qualitative decision making.
Declarative Representation of Revision Strategies
Mar 08, 2000Abstract:In this paper we introduce a nonmonotonic framework for belief revision in which reasoning about the reliability of different pieces of information based on meta-knowledge about the information is possible, and where revision strategies can be described declaratively. The approach is based on a Poole-style system for default reasoning in which entrenchment information is represented in the logical language. A notion of inference based on the least fixed point of a monotone operator is used to make sure that all theories possess a consistent set of conclusions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge