A Memory Transformer Network for Incremental Learning

We study class-incremental learning, a training setup in which new classes of data are observed over time for the model to learn from. Despite the straightforward problem formulation, the naive application of classification models to class-incremental learning results in the "catastrophic forgetting" of previously seen classes. One of the most successful existing methods has been the use of a memory of exemplars, which overcomes the issue of catastrophic forgetting by saving a subset of past data into a memory bank and utilizing it to prevent forgetting when training future tasks. In our paper, we propose to enhance the utilization of this memory bank: we not only use it as a source of additional training data like existing works but also integrate it in the prediction process explicitly.Our method, the Memory Transformer Network (MTN), learns how to combine and aggregate the information from the nearest neighbors in the memory with a transformer to make more accurate predictions. We conduct extensive experiments and ablations to evaluate our approach. We show that MTN achieves state-of-the-art performance on the challenging ImageNet-1k and Google-Landmarks-1k incremental learning benchmarks.

3D Scene Compression through Entropy Penalized Neural Representation Functions

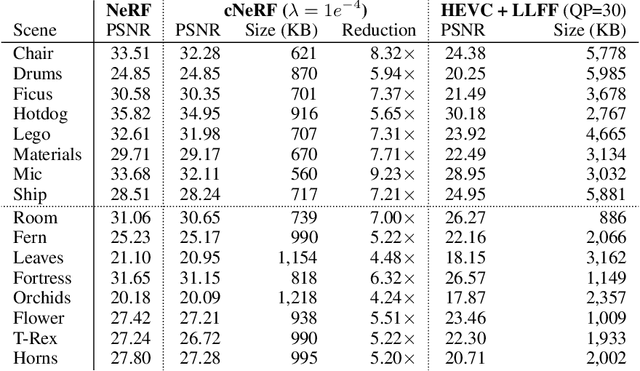
Some forms of novel visual media enable the viewer to explore a 3D scene from arbitrary viewpoints, by interpolating between a discrete set of original views. Compared to 2D imagery, these types of applications require much larger amounts of storage space, which we seek to reduce. Existing approaches for compressing 3D scenes are based on a separation of compression and rendering: each of the original views is compressed using traditional 2D image formats; the receiver decompresses the views and then performs the rendering. We unify these steps by directly compressing an implicit representation of the scene, a function that maps spatial coordinates to a radiance vector field, which can then be queried to render arbitrary viewpoints. The function is implemented as a neural network and jointly trained for reconstruction as well as compressibility, in an end-to-end manner, with the use of an entropy penalty on the parameters. Our method significantly outperforms a state-of-the-art conventional approach for scene compression, achieving simultaneously higher quality reconstructions and lower bitrates. Furthermore, we show that the performance at lower bitrates can be improved by jointly representing multiple scenes using a soft form of parameter sharing.

Reducing the Computational Cost of Deep Generative Models with Binary Neural Networks

Deep generative models provide a powerful set of tools to understand real-world data. But as these models improve, they increase in size and complexity, so their computational cost in memory and execution time grows. Using binary weights in neural networks is one method which has shown promise in reducing this cost. However, whether binary neural networks can be used in generative models is an open problem. In this work we show, for the first time, that we can successfully train generative models which utilize binary neural networks. This reduces the computational cost of the models massively. We develop a new class of binary weight normalization, and provide insights for architecture designs of these binarized generative models. We demonstrate that two state-of-the-art deep generative models, the ResNet VAE and Flow++ models, can be binarized effectively using these techniques. We train binary models that achieve loss values close to those of the regular models but are 90%-94% smaller in size, and also allow significant speed-ups in execution time.

HiLLoC: Lossless Image Compression with Hierarchical Latent Variable Models

We make the following striking observation: fully convolutional VAE models trained on 32x32 ImageNet can generalize well, not just to 64x64 but also to far larger photographs, with no changes to the model. We use this property, applying fully convolutional models to lossless compression, demonstrating a method to scale the VAE-based 'Bits-Back with ANS' algorithm for lossless compression to large color photographs, and achieving state of the art for compression of full size ImageNet images. We release Craystack, an open source library for convenient prototyping of lossless compression using probabilistic models, along with full implementations of all of our compression results.

Variational f-divergence Minimization

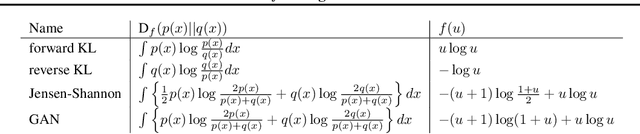
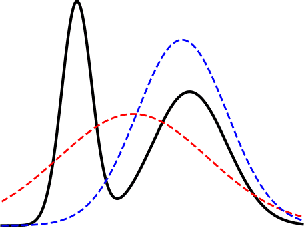
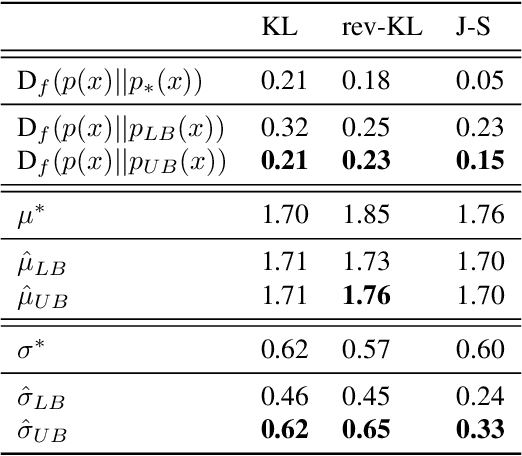
Probabilistic models are often trained by maximum likelihood, which corresponds to minimizing a specific f-divergence between the model and data distribution. In light of recent successes in training Generative Adversarial Networks, alternative non-likelihood training criteria have been proposed. Whilst not necessarily statistically efficient, these alternatives may better match user requirements such as sharp image generation. A general variational method for training probabilistic latent variable models using maximum likelihood is well established; however, how to train latent variable models using other f-divergences is comparatively unknown. We discuss a variational approach that, when combined with the recently introduced Spread Divergence, can be applied to train a large class of latent variable models using any f-divergence.

Spread Divergences

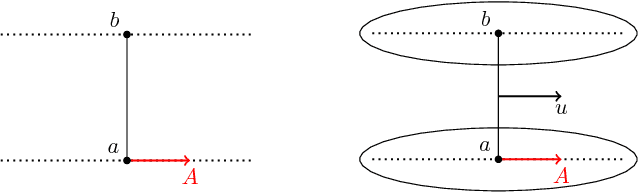
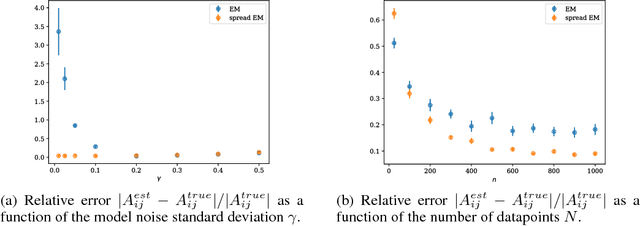
For distributions p and q with different support, the divergence generally will not exist. We define a spread divergence on modified p and q and describe sufficient conditions for the existence of such a divergence. We give examples of using a spread divergence to train implicit generative models, including linear models (Principal Components Analysis and Independent Components Analysis) and non-linear models (Deep Generative Networks).

Stochastic Variational Optimization

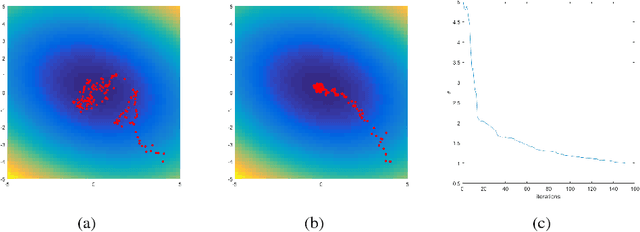
Variational Optimization forms a differentiable upper bound on an objective. We show that approaches such as Natural Evolution Strategies and Gaussian Perturbation, are special cases of Variational Optimization in which the expectations are approximated by Gaussian sampling. These approaches are of particular interest because they are parallelizable. We calculate the approximate bias and variance of the corresponding gradient estimators and demonstrate that using antithetic sampling or a baseline is crucial to mitigate their problems. We contrast these methods with an alternative parallelizable method, namely Directional Derivatives. We conclude that, for differentiable objectives, using Directional Derivatives is preferable to using Variational Optimization to perform parallel Stochastic Gradient Descent.