Free-breathing 3D cardiac extracellular volume (ECV) mapping using a linear tangent space alignment (LTSA) model

$\textbf{Purpose:}$ To develop a new method for free-breathing 3D extracellular volume (ECV) mapping of the whole heart at 3T. $\textbf{Methods:}$ A free-breathing 3D cardiac ECV mapping method was developed at 3T. T1 mapping was performed before and after contrast agent injection using a free-breathing ECG-gated inversion-recovery sequence with spoiled gradient echo readout. A linear tangent space alignment (LTSA) model-based method was used to reconstruct high-frame-rate dynamic images from (k,t)-space data sparsely sampled along a random stack-of-stars trajectory. Joint T1 and transmit B1 estimation was performed voxel-by-voxel for pre- and post-contrast T1 mapping. To account for the time-varying T1 after contrast agent injection, a linearly time-varying T1 model was introduced for post-contrast T1 mapping. ECV maps were generated by aligning pre- and post-contrast T1 maps through affine transformation. $\textbf{Results:}$ The feasibility of the proposed method was demonstrated using in vivo studies with six healthy volunteers at 3T. We obtained 3D ECV maps at a spatial resolution of 1.9$\times$1.9$\times$4.5 $mm^{3}$ and a FOV of 308$\times$308$\times$144 $mm^{3}$, with a scan time of 10.1$\pm$1.4 and 10.6$\pm$1.6 min before and after contrast agent injection, respectively. The ECV maps and the pre- and post-contrast T1 maps obtained by the proposed method were in good agreement with the 2D MOLLI method both qualitatively and quantitatively. $\textbf{Conclusion:}$ The proposed method allows for free-breathing 3D ECV mapping of the whole heart within a practically feasible imaging time. The estimated ECV values from the proposed method were comparable to those from the existing method. $\textbf{Keywords:}$ cardiac extracellular volume (ECV) mapping, cardiac T1 mapping, linear tangent space alignment (LTSA), manifold learning

Posterior Estimation for Dynamic PET imaging using Conditional Variational Inference

This work aims efficiently estimating the posterior distribution of kinetic parameters for dynamic positron emission tomography (PET) imaging given a measurement of time of activity curve. Considering the inherent information loss from parametric imaging to measurement space with the forward kinetic model, the inverse mapping is ambiguous. The conventional (but expensive) solution can be the Markov Chain Monte Carlo (MCMC) sampling, which is known to produce unbiased asymptotical estimation. We propose a deep-learning-based framework for efficient posterior estimation. Specifically, we counteract the information loss in the forward process by introducing latent variables. Then, we use a conditional variational autoencoder (CVAE) and optimize its evidence lower bound. The well-trained decoder is able to infer the posterior with a given measurement and the sampled latent variables following a simple multivariate Gaussian distribution. We validate our CVAE-based method using unbiased MCMC as the reference for low-dimensional data (a single brain region) with the simplified reference tissue model.

Posterior Estimation Using Deep Learning: A Simulation Study of Compartmental Modeling in Dynamic PET

Background: In medical imaging, images are usually treated as deterministic, while their uncertainties are largely underexplored. Purpose: This work aims at using deep learning to efficiently estimate posterior distributions of imaging parameters, which in turn can be used to derive the most probable parameters as well as their uncertainties. Methods: Our deep learning-based approaches are based on a variational Bayesian inference framework, which is implemented using two different deep neural networks based on conditional variational auto-encoder (CVAE), CVAE-dual-encoder and CVAE-dual-decoder. The conventional CVAE framework, i.e., CVAE-vanilla, can be regarded as a simplified case of these two neural networks. We applied these approaches to a simulation study of dynamic brain PET imaging using a reference region-based kinetic model. Results: In the simulation study, we estimated posterior distributions of PET kinetic parameters given a measurement of time-activity curve. Our proposed CVAE-dual-encoder and CVAE-dual-decoder yield results that are in good agreement with the asymptotically unbiased posterior distributions sampled by Markov Chain Monte Carlo (MCMC). The CVAE-vanilla can also be used for estimating posterior distributions, although it has an inferior performance to both CVAE-dual-encoder and CVAE-dual-decoder. Conclusions: We have evaluated the performance of our deep learning approaches for estimating posterior distributions in dynamic brain PET. Our deep learning approaches yield posterior distributions, which are in good agreement with unbiased distributions estimated by MCMC. All these neural networks have different characteristics and can be chosen by the user for specific applications. The proposed methods are general and can be adapted to other problems.

Variational Inference for Quantifying Inter-observer Variability in Segmentation of Anatomical Structures

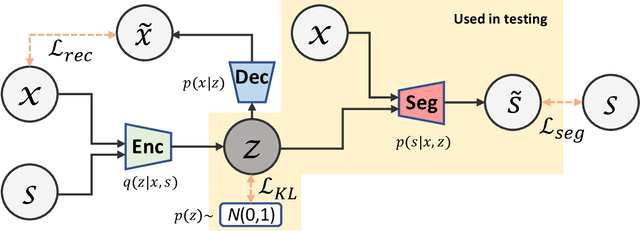
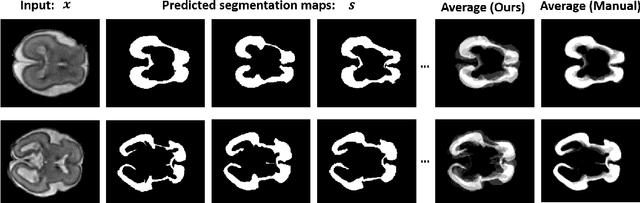
Lesions or organ boundaries visible through medical imaging data are often ambiguous, thus resulting in significant variations in multi-reader delineations, i.e., the source of aleatoric uncertainty. In particular, quantifying the inter-observer variability of manual annotations with Magnetic Resonance (MR) Imaging data plays a crucial role in establishing a reference standard for various diagnosis and treatment tasks. Most segmentation methods, however, simply model a mapping from an image to its single segmentation map and do not take the disagreement of annotators into consideration. In order to account for inter-observer variability, without sacrificing accuracy, we propose a novel variational inference framework to model the distribution of plausible segmentation maps, given a specific MR image, which explicitly represents the multi-reader variability. Specifically, we resort to a latent vector to encode the multi-reader variability and counteract the inherent information loss in the imaging data. Then, we apply a variational autoencoder network and optimize its evidence lower bound (ELBO) to efficiently approximate the distribution of the segmentation map, given an MR image. Experimental results, carried out with the QUBIQ brain growth MRI segmentation datasets with seven annotators, demonstrate the effectiveness of our approach.