Adversarial training for predictive tasks: theoretical analysis and limitations in the deterministic case

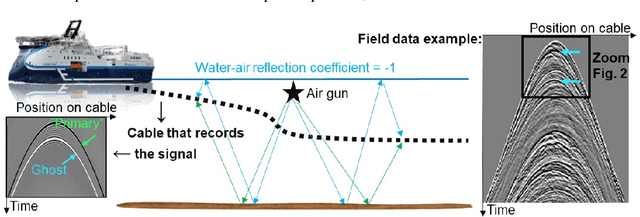
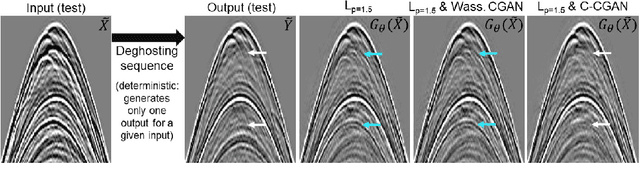
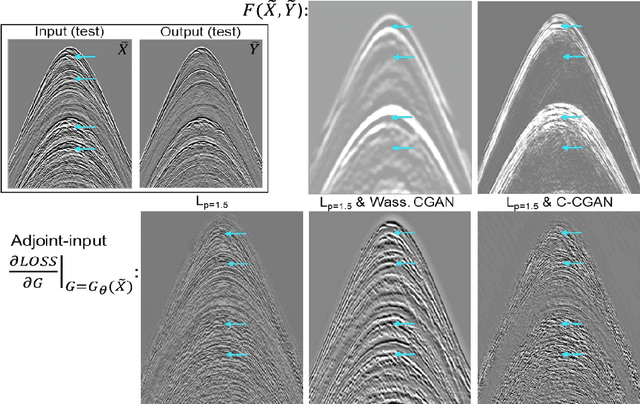
To train a deep neural network to mimic the outcomes of processing sequences, a version of Conditional Generalized Adversarial Network (CGAN) can be used. It has been observed by others that CGAN can help to improve the results even for deterministic sequences, where only one output is associated with the processing of a given input. Surprisingly, our CGAN-based tests on deterministic geophysical processing sequences did not produce a real improvement compared to the use of an $L_p$ loss; we here propose a first theoretical explanation why. Our analysis goes from the non-deterministic case to the deterministic one. It led us to develop an adversarial way to train a content loss that gave better results on our data.

Phase transitions and optimal algorithms in high-dimensional Gaussian mixture clustering

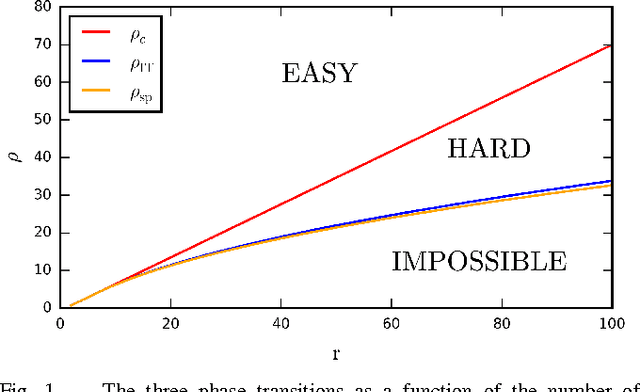
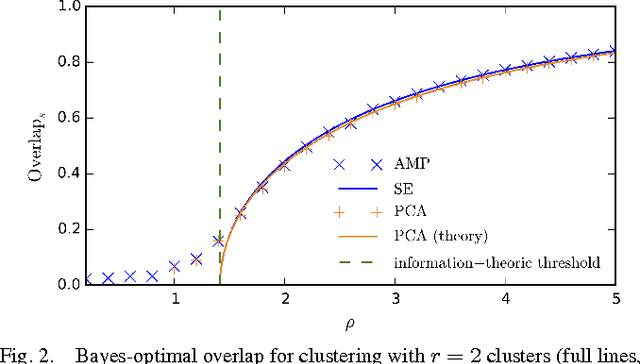
We consider the problem of Gaussian mixture clustering in the high-dimensional limit where the data consists of $m$ points in $n$ dimensions, $n,m \rightarrow \infty$ and $\alpha = m/n$ stays finite. Using exact but non-rigorous methods from statistical physics, we determine the critical value of $\alpha$ and the distance between the clusters at which it becomes information-theoretically possible to reconstruct the membership into clusters better than chance. We also determine the accuracy achievable by the Bayes-optimal estimation algorithm. In particular, we find that when the number of clusters is sufficiently large, $r > 4 + 2 \sqrt{\alpha}$, there is a gap between the threshold for information-theoretically optimal performance and the threshold at which known algorithms succeed.

Mutual information for symmetric rank-one matrix estimation: A proof of the replica formula

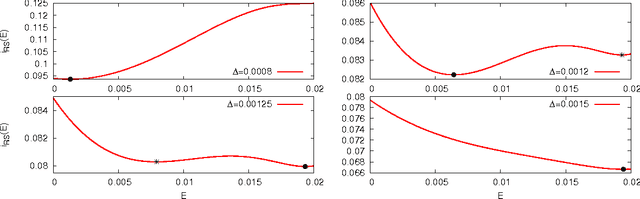
Factorizing low-rank matrices has many applications in machine learning and statistics. For probabilistic models in the Bayes optimal setting, a general expression for the mutual information has been proposed using heuristic statistical physics computations, and proven in few specific cases. Here, we show how to rigorously prove the conjectured formula for the symmetric rank-one case. This allows to express the minimal mean-square-error and to characterize the detectability phase transitions in a large set of estimation problems ranging from community detection to sparse PCA. We also show that for a large set of parameters, an iterative algorithm called approximate message-passing is Bayes optimal. There exists, however, a gap between what currently known polynomial algorithms can do and what is expected information theoretically. Additionally, the proof technique has an interest of its own and exploits three essential ingredients: the interpolation method introduced in statistical physics by Guerra, the analysis of the approximate message-passing algorithm and the theory of spatial coupling and threshold saturation in coding. Our approach is generic and applicable to other open problems in statistical estimation where heuristic statistical physics predictions are available.

MMSE of probabilistic low-rank matrix estimation: Universality with respect to the output channel

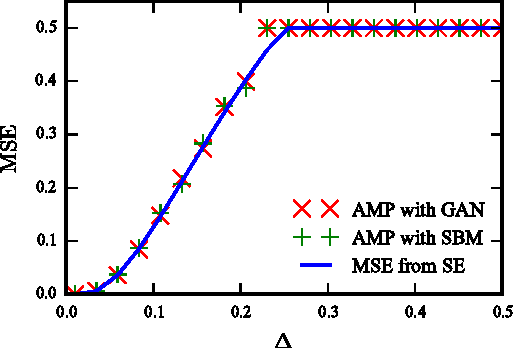
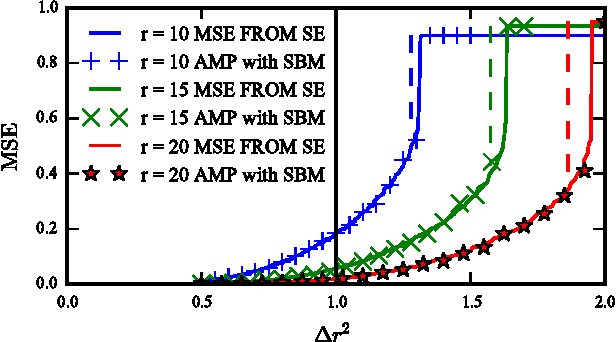
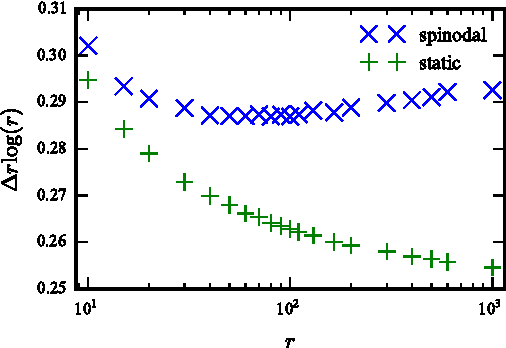
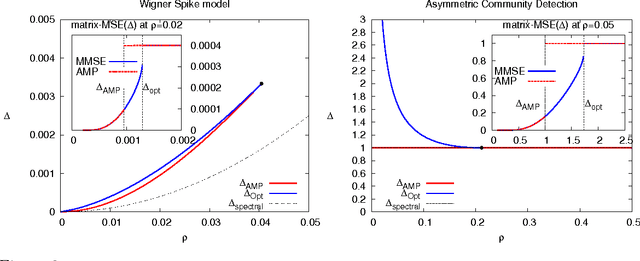
This paper considers probabilistic estimation of a low-rank matrix from non-linear element-wise measurements of its elements. We derive the corresponding approximate message passing (AMP) algorithm and its state evolution. Relying on non-rigorous but standard assumptions motivated by statistical physics, we characterize the minimum mean squared error (MMSE) achievable information theoretically and with the AMP algorithm. Unlike in related problems of linear estimation, in the present setting the MMSE depends on the output channel only trough a single parameter - its Fisher information. We illustrate this striking finding by analysis of submatrix localization, and of detection of communities hidden in a dense stochastic block model. For this example we locate the computational and statistical boundaries that are not equal for rank larger than four.

Phase Transitions in Sparse PCA

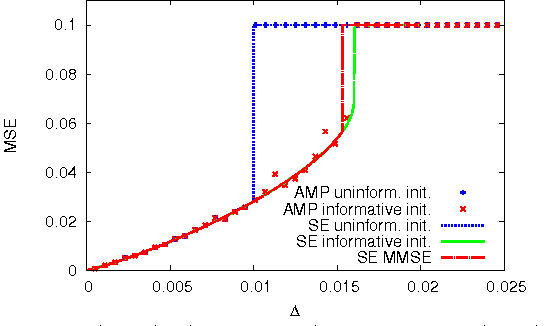
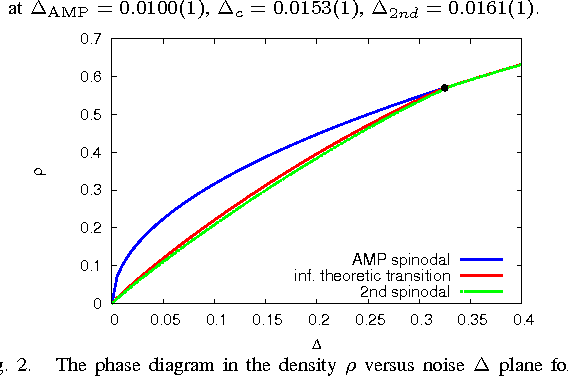
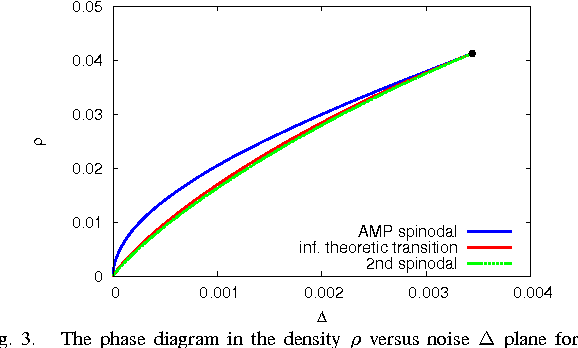
We study optimal estimation for sparse principal component analysis when the number of non-zero elements is small but on the same order as the dimension of the data. We employ approximate message passing (AMP) algorithm and its state evolution to analyze what is the information theoretically minimal mean-squared error and the one achieved by AMP in the limit of large sizes. For a special case of rank one and large enough density of non-zeros Deshpande and Montanari [1] proved that AMP is asymptotically optimal. We show that both for low density and for large rank the problem undergoes a series of phase transitions suggesting existence of a region of parameters where estimation is information theoretically possible, but AMP (and presumably every other polynomial algorithm) fails. The analysis of the large rank limit is particularly instructive.