Mutual information for symmetric rank-one matrix estimation: A proof of the replica formula
Paper and Code
Jun 13, 2016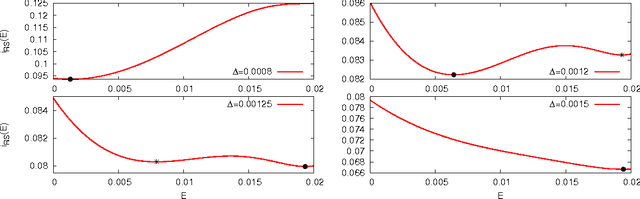
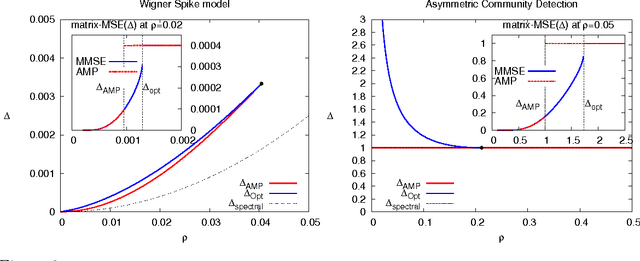
Factorizing low-rank matrices has many applications in machine learning and statistics. For probabilistic models in the Bayes optimal setting, a general expression for the mutual information has been proposed using heuristic statistical physics computations, and proven in few specific cases. Here, we show how to rigorously prove the conjectured formula for the symmetric rank-one case. This allows to express the minimal mean-square-error and to characterize the detectability phase transitions in a large set of estimation problems ranging from community detection to sparse PCA. We also show that for a large set of parameters, an iterative algorithm called approximate message-passing is Bayes optimal. There exists, however, a gap between what currently known polynomial algorithms can do and what is expected information theoretically. Additionally, the proof technique has an interest of its own and exploits three essential ingredients: the interpolation method introduced in statistical physics by Guerra, the analysis of the approximate message-passing algorithm and the theory of spatial coupling and threshold saturation in coding. Our approach is generic and applicable to other open problems in statistical estimation where heuristic statistical physics predictions are available.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge