Galaxy Image Simulation Using Progressive GANs

In this work, we provide an efficient and realistic data-driven approach to simulate astronomical images using deep generative models from machine learning. Our solution is based on a variant of the generative adversarial network (GAN) with progressive training methodology and Wasserstein cost function. The proposed solution generates naturalistic images of galaxies that show complex structures and high diversity, which suggests that data-driven simulations using machine learning can replace many of the expensive model-driven methods used in astronomical data processing.

Rank-one matrix estimation: analysis of algorithmic and information theoretic limits by the spatial coupling method

Factorizing low-rank matrices is a problem with many applications in machine learning and statistics, ranging from sparse PCA to community detection and sub-matrix localization. For probabilistic models in the Bayes optimal setting, general expressions for the mutual information have been proposed using powerful heuristic statistical physics computations via the replica and cavity methods, and proven in few specific cases by a variety of methods. Here, we use the spatial coupling methodology developed in the framework of error correcting codes, to rigorously derive the mutual information for the symmetric rank-one case. We characterize the detectability phase transitions in a large set of estimation problems, where we show that there exists a gap between what currently known polynomial algorithms (in particular spectral methods and approximate message-passing) can do and what is expected information theoretically. Moreover, we show that the computational gap vanishes for the proposed spatially coupled model, a promising feature with many possible applications. Our proof technique has an interest on its own and exploits three essential ingredients: the interpolation method first introduced in statistical physics, the analysis of approximate message-passing algorithms first introduced in compressive sensing, and the theory of threshold saturation for spatially coupled systems first developed in coding theory. Our approach is very generic and can be applied to many other open problems in statistical estimation where heuristic statistical physics predictions are available.

Mutual information for symmetric rank-one matrix estimation: A proof of the replica formula

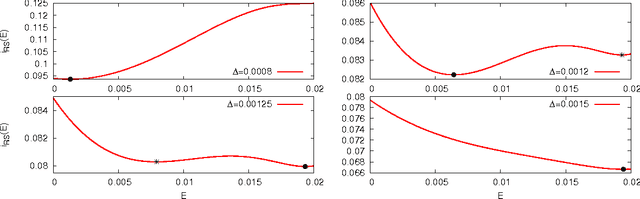
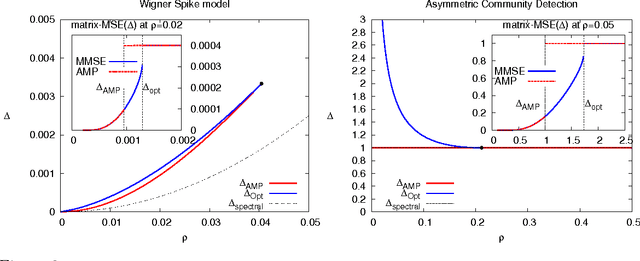
Factorizing low-rank matrices has many applications in machine learning and statistics. For probabilistic models in the Bayes optimal setting, a general expression for the mutual information has been proposed using heuristic statistical physics computations, and proven in few specific cases. Here, we show how to rigorously prove the conjectured formula for the symmetric rank-one case. This allows to express the minimal mean-square-error and to characterize the detectability phase transitions in a large set of estimation problems ranging from community detection to sparse PCA. We also show that for a large set of parameters, an iterative algorithm called approximate message-passing is Bayes optimal. There exists, however, a gap between what currently known polynomial algorithms can do and what is expected information theoretically. Additionally, the proof technique has an interest of its own and exploits three essential ingredients: the interpolation method introduced in statistical physics by Guerra, the analysis of the approximate message-passing algorithm and the theory of spatial coupling and threshold saturation in coding. Our approach is generic and applicable to other open problems in statistical estimation where heuristic statistical physics predictions are available.