MMSE of probabilistic low-rank matrix estimation: Universality with respect to the output channel
Paper and Code
Jan 05, 2016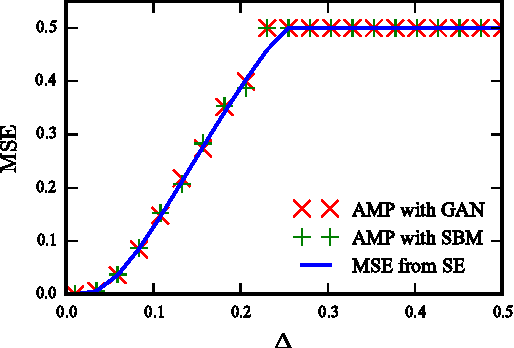
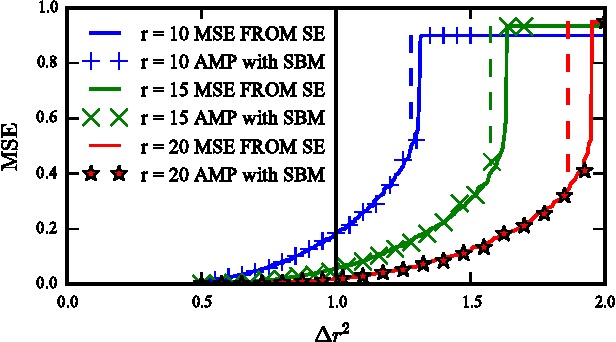
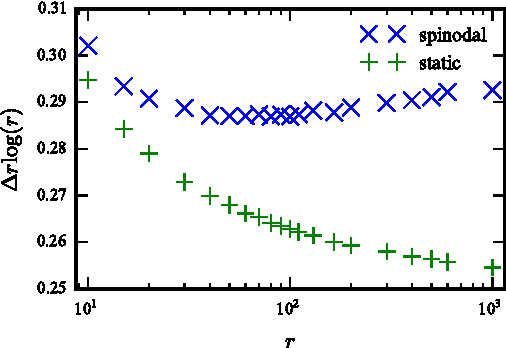
This paper considers probabilistic estimation of a low-rank matrix from non-linear element-wise measurements of its elements. We derive the corresponding approximate message passing (AMP) algorithm and its state evolution. Relying on non-rigorous but standard assumptions motivated by statistical physics, we characterize the minimum mean squared error (MMSE) achievable information theoretically and with the AMP algorithm. Unlike in related problems of linear estimation, in the present setting the MMSE depends on the output channel only trough a single parameter - its Fisher information. We illustrate this striking finding by analysis of submatrix localization, and of detection of communities hidden in a dense stochastic block model. For this example we locate the computational and statistical boundaries that are not equal for rank larger than four.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge