ICML Topological Deep Learning Challenge 2024: Beyond the Graph Domain

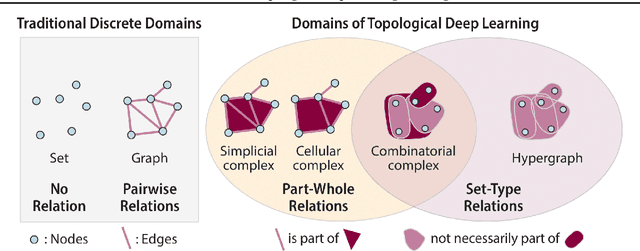
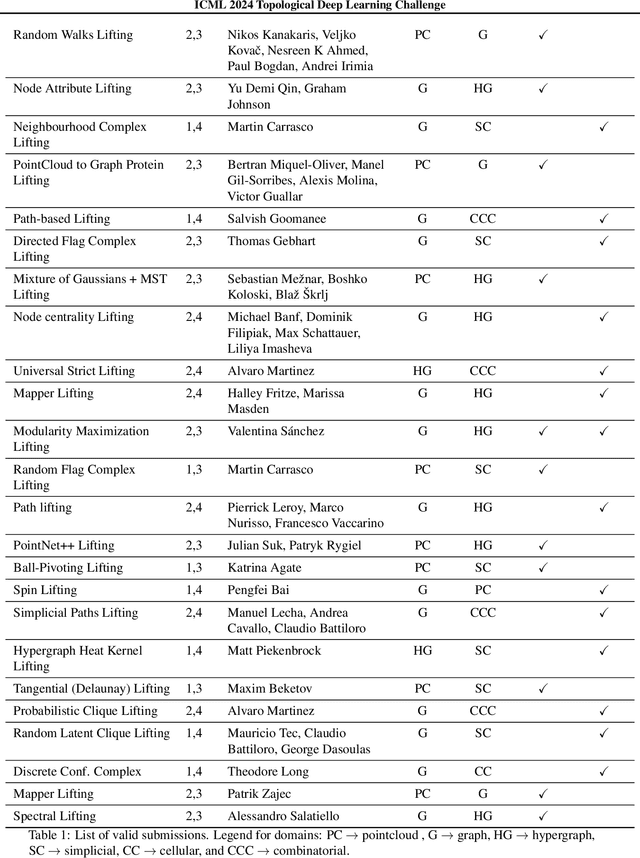
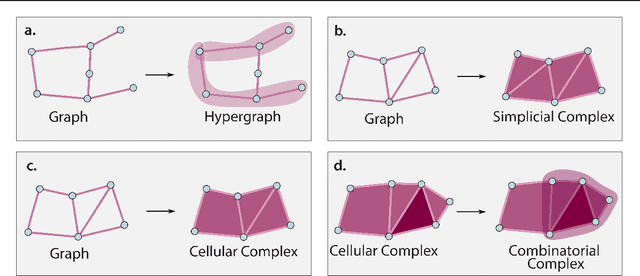
This paper describes the 2nd edition of the ICML Topological Deep Learning Challenge that was hosted within the ICML 2024 ELLIS Workshop on Geometry-grounded Representation Learning and Generative Modeling (GRaM). The challenge focused on the problem of representing data in different discrete topological domains in order to bridge the gap between Topological Deep Learning (TDL) and other types of structured datasets (e.g. point clouds, graphs). Specifically, participants were asked to design and implement topological liftings, i.e. mappings between different data structures and topological domains --like hypergraphs, or simplicial/cell/combinatorial complexes. The challenge received 52 submissions satisfying all the requirements. This paper introduces the main scope of the challenge, and summarizes the main results and findings.

Geodesic Mode Connectivity

Mode connectivity is a phenomenon where trained models are connected by a path of low loss. We reframe this in the context of Information Geometry, where neural networks are studied as spaces of parameterized distributions with curved geometry. We hypothesize that shortest paths in these spaces, known as geodesics, correspond to mode-connecting paths in the loss landscape. We propose an algorithm to approximate geodesics and demonstrate that they achieve mode connectivity.