Diverse Neural Sequences in QIF Networks: An Analytically Tractable Framework for Synfire Chains and Hippocampal Replay

Sequential neural activity is fundamental to cognition, yet how diverse sequences are recalled under biological constraints remains a key question. Existing models often struggle to balance biophysical realism and analytical tractability. We address this problem by proposing a parsimonious network of Quadratic Integrate-and-Fire (QIF) neurons with sequences embedded via a temporally asymmetric Hebbian (TAH) rule. Our findings demonstrate that this single framework robustly reproduces a spectrum of sequential activities, including persistent synfire-like chains and transient, hippocampal replay-like bursts exhibiting intra-ripple frequency accommodation (IFA), all achieved without requiring specialized delay or adaptation mechanisms. Crucially, we derive exact low-dimensional firing-rate equations (FREs) that provide mechanistic insight, elucidating the bifurcation structure governing these distinct dynamical regimes and explaining their stability. The model also exhibits strong robustness to synaptic heterogeneity and memory pattern overlap. These results establish QIF networks with TAH connectivity as an analytically tractable and biologically plausible platform for investigating the emergence, stability, and diversity of sequential neural activity in the brain.

A provable control of sensitivity of neural networks through a direct parameterization of the overall bi-Lipschitzness

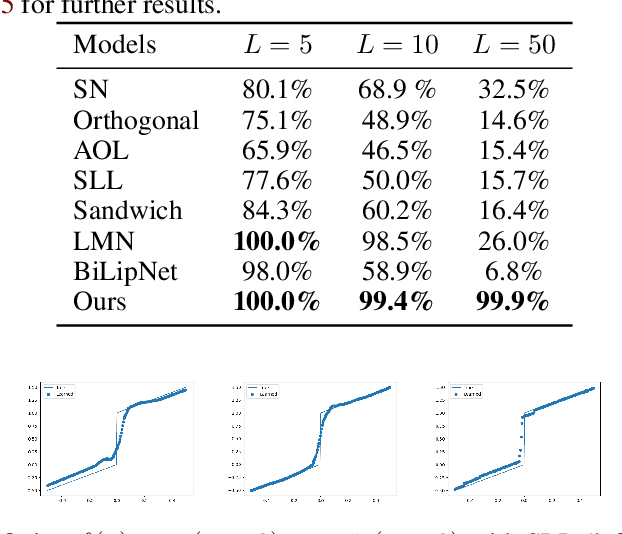
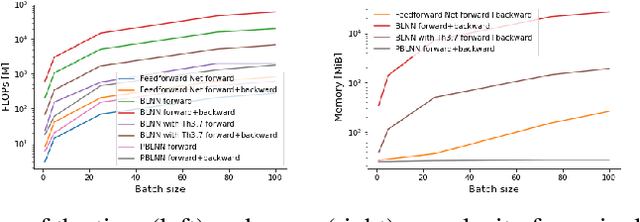
While neural networks can enjoy an outstanding flexibility and exhibit unprecedented performance, the mechanism behind their behavior is still not well-understood. To tackle this fundamental challenge, researchers have tried to restrict and manipulate some of their properties in order to gain new insights and better control on them. Especially, throughout the past few years, the concept of \emph{bi-Lipschitzness} has been proved as a beneficial inductive bias in many areas. However, due to its complexity, the design and control of bi-Lipschitz architectures are falling behind, and a model that is precisely designed for bi-Lipschitzness realizing a direct and simple control of the constants along with solid theoretical analysis is lacking. In this work, we investigate and propose a novel framework for bi-Lipschitzness that can achieve such a clear and tight control based on convex neural networks and the Legendre-Fenchel duality. Its desirable properties are illustrated with concrete experiments. We also apply this framework to uncertainty estimation and monotone problem settings to illustrate its broad range of applications.

Causal Graph in Language Model Rediscovers Cortical Hierarchy in Human Narrative Processing

Understanding how humans process natural language has long been a vital research direction. The field of natural language processing (NLP) has recently experienced a surge in the development of powerful language models. These models have proven to be invaluable tools for studying another complex system known to process human language: the brain. Previous studies have demonstrated that the features of language models can be mapped to fMRI brain activity. This raises the question: is there a commonality between information processing in language models and the human brain? To estimate information flow patterns in a language model, we examined the causal relationships between different layers. Drawing inspiration from the workspace framework for consciousness, we hypothesized that features integrating more information would more accurately predict higher hierarchical brain activity. To validate this hypothesis, we classified language model features into two categories based on causal network measures: 'low in-degree' and 'high in-degree'. We subsequently compared the brain prediction accuracy maps for these two groups. Our results reveal that the difference in prediction accuracy follows a hierarchical pattern, consistent with the cortical hierarchy map revealed by activity time constants. This finding suggests a parallel between how language models and the human brain process linguistic information.

Spontaneous Emerging Preference in Two-tower Language Model

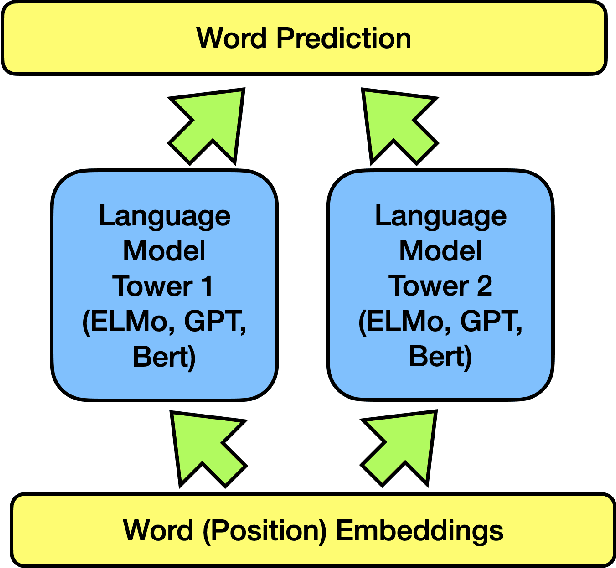
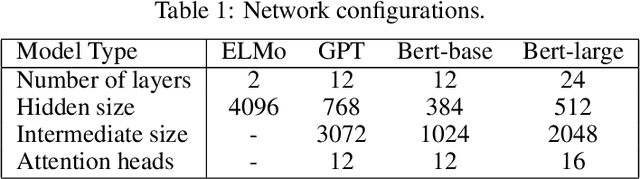
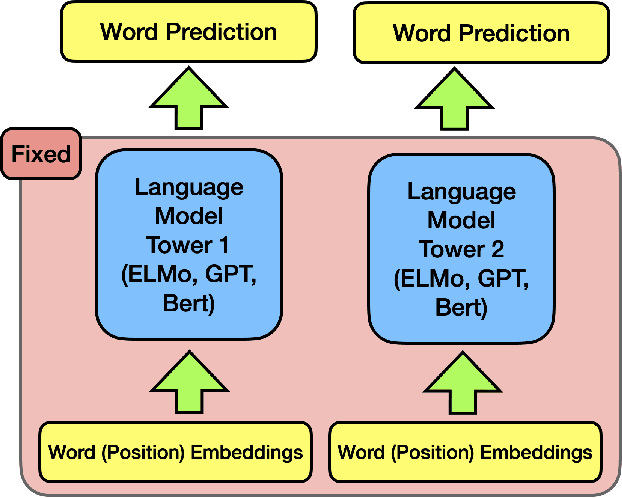
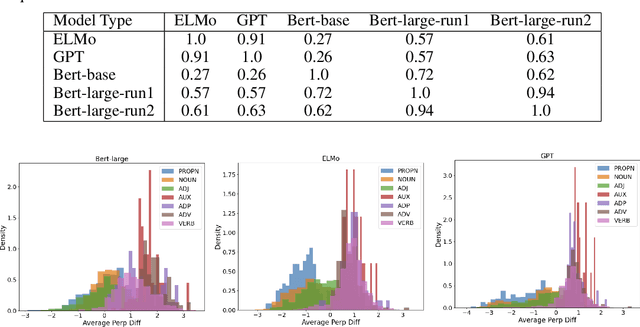
The ever-growing size of the foundation language model has brought significant performance gains in various types of downstream tasks. With the existence of side-effects brought about by the large size of the foundation language model such as deployment cost, availability issues, and environmental cost, there is some interest in exploring other possible directions, such as a divide-and-conquer scheme. In this paper, we are asking a basic question: are language processes naturally dividable? We study this problem with a simple two-tower language model setting, where two language models with identical configurations are trained side-by-side cooperatively. With this setting, we discover the spontaneous emerging preference phenomenon, where some of the tokens are consistently better predicted by one tower while others by another tower. This phenomenon is qualitatively stable, regardless of model configuration and type, suggesting this as an intrinsic property of natural language. This study suggests that interesting properties of natural language are still waiting to be discovered, which may aid the future development of natural language processing techniques.

An Information-theoretic Progressive Framework for Interpretation

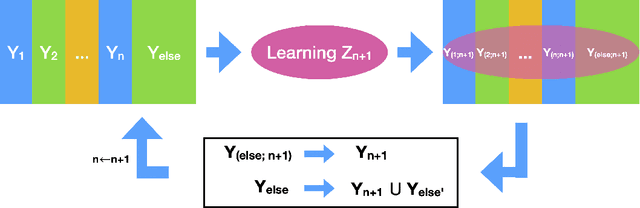
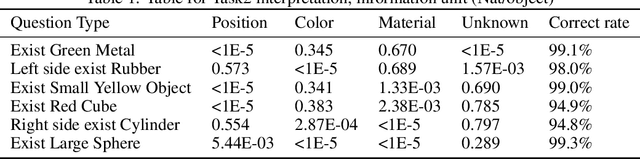
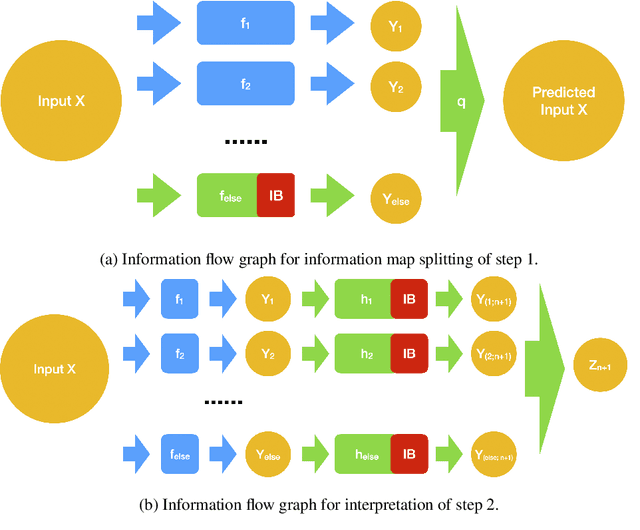
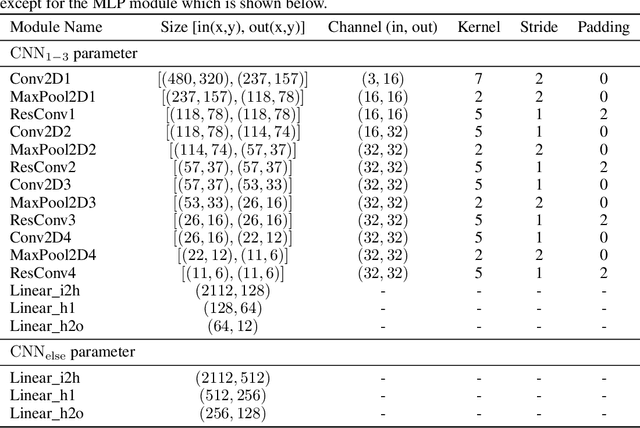
Both brain science and the deep learning communities have the problem of interpreting neural activity. For deep learning, even though we can access all neurons' activity data, interpretation of how the deep network solves the task is still challenging. Although a large amount of effort has been devoted to interpreting a deep network, there is still no consensus of what interpretation is. This paper tries to push the discussion in this direction and proposes an information-theoretic progressive framework to synthesize interpretation. Firstly, we discuss intuitions of interpretation: interpretation is meta-information; interpretation should be at the right level; inducing independence is helpful to interpretation; interpretation is naturally progressive; interpretation doesn't have to involve a human. Then, we build the framework with an information map splitting idea and implement it with the variational information bottleneck technique. After that, we test the framework with the CLEVR dataset. The framework is shown to be able to split information maps and synthesize interpretation in the form of meta-information.

Dimensionality reduction to maximize prediction generalization capability

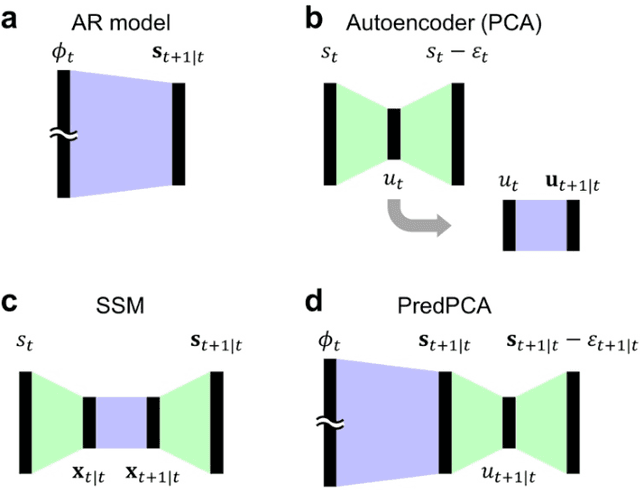
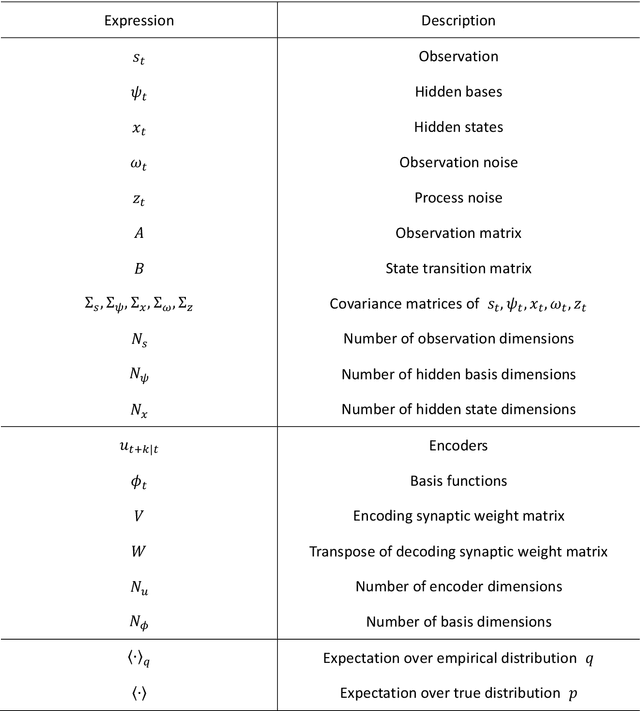
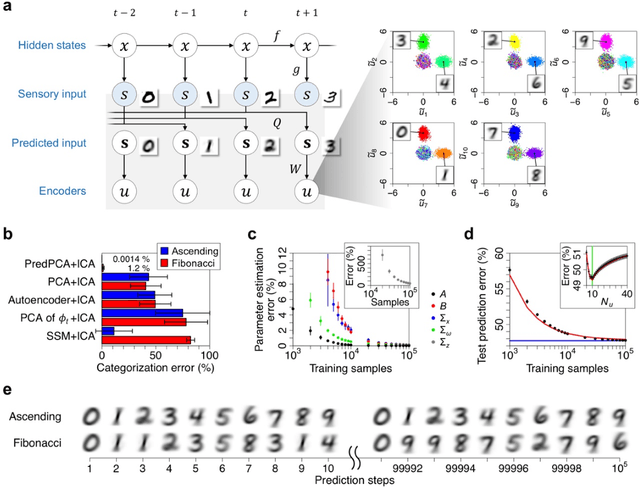
This work develops an analytically solvable unsupervised learning scheme that extracts the most informative components for predicting future inputs, termed predictive principal component analysis (PredPCA). Our scheme can effectively remove unpredictable observation noise and globally minimize the test prediction error. Mathematical analyses demonstrate that, with sufficiently high-dimensional observations that are generated by a linear or nonlinear system, PredPCA can identify the optimal hidden state representation, true system parameters, and true hidden state dimensionality, with a global convergence guarantee. We demonstrate the performance of PredPCA by using sequential visual inputs comprising hand-digits, rotating 3D objects, and natural scenes. It reliably and accurately estimates distinct hidden states and predicts future outcomes of previously unseen test input data, even in the presence of considerable observation noise. The simple model structure and low computational cost of PredPCA make it highly desirable as a learning scheme for biological neural networks and neuromorphic chips.

On the achievability of blind source separation for high-dimensional nonlinear source mixtures

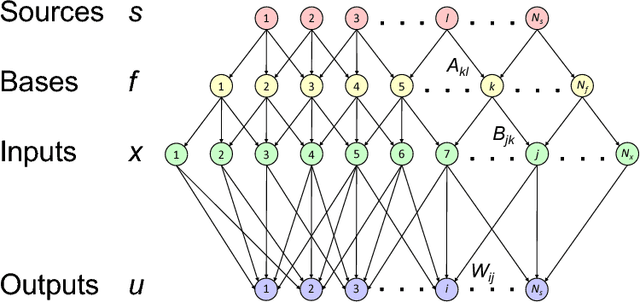
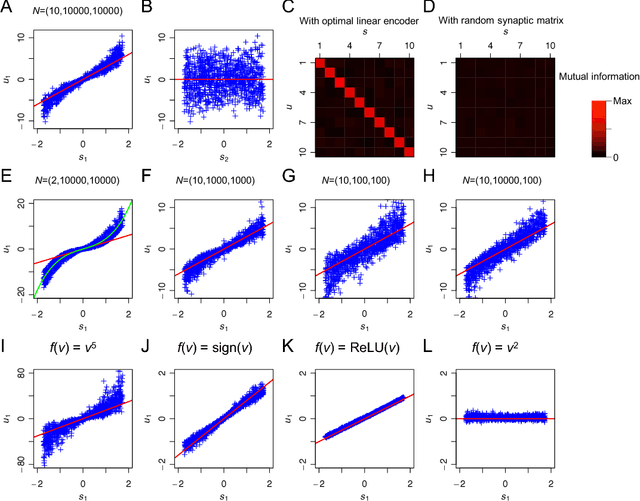
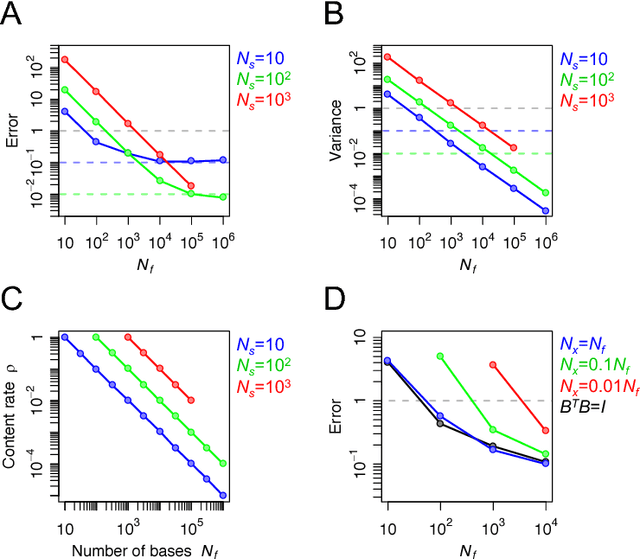
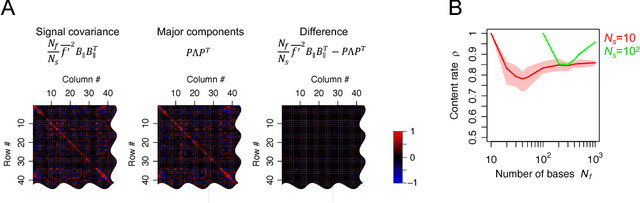
For many years, a combination of principal component analysis (PCA) and independent component analysis (ICA) has been used as a blind source separation (BSS) technique to separate hidden sources of natural data. However, it is unclear why these linear methods work well because most real-world data involve nonlinear mixtures of sources. We show that a cascade of PCA and ICA can solve this nonlinear BSS problem accurately as the variety of input signals increases. Specifically, we present two theorems that guarantee asymptotically zero-error BSS when sources are mixed by a feedforward network with two processing layers. Our first theorem analytically quantifies the performance of an optimal linear encoder that reconstructs independent sources. Zero-error is asymptotically reached when the number of sources is large and the numbers of inputs and nonlinear bases are large relative to the number of sources. The next question involves finding an optimal linear encoder without observing the underlying sources. Our second theorem guarantees that PCA can reliably extract all the subspace represented by the optimal linear encoder, so that a subsequent application of ICA can separate all sources. Thereby, for almost all nonlinear generative processes with sufficient variety, the cascade of PCA and ICA performs asymptotically zero-error BSS in an unsupervised manner. We analytically and numerically validate the theorems. These results highlight the utility of linear BSS techniques for accurately recovering nonlinearly mixed sources when observations are sufficiently diverse. We also discuss a possible biological BSS implementation.

Reinforced stochastic gradient descent for deep neural network learning

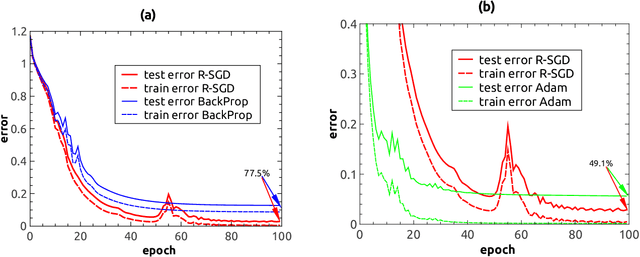
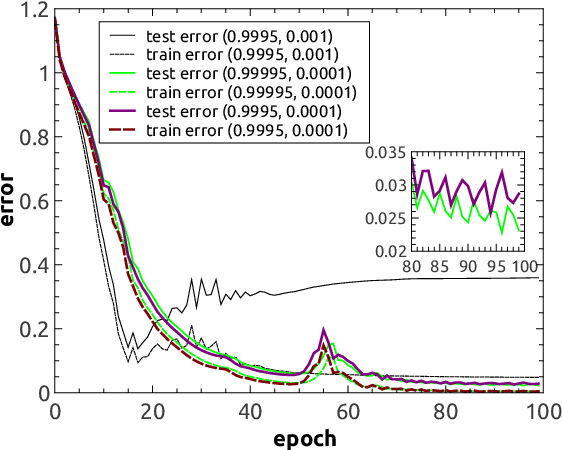
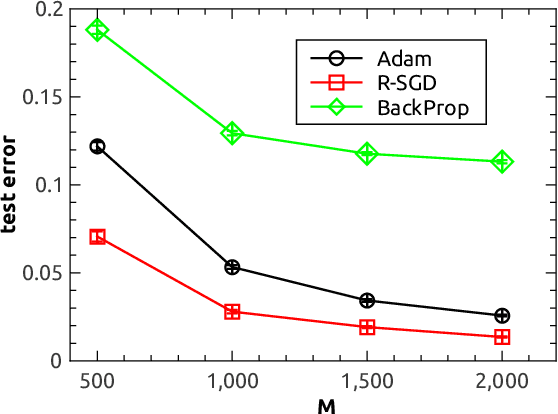
Stochastic gradient descent (SGD) is a standard optimization method to minimize a training error with respect to network parameters in modern neural network learning. However, it typically suffers from proliferation of saddle points in the high-dimensional parameter space. Therefore, it is highly desirable to design an efficient algorithm to escape from these saddle points and reach a parameter region of better generalization capabilities. Here, we propose a simple extension of SGD, namely reinforced SGD, which simply adds previous first-order gradients in a stochastic manner with a probability that increases with learning time. As verified in a simple synthetic dataset, this method significantly accelerates learning compared with the original SGD. Surprisingly, it dramatically reduces over-fitting effects, even compared with state-of-the-art adaptive learning algorithm---Adam. For a benchmark handwritten digits dataset, the learning performance is comparable to Adam, yet with an extra advantage of requiring one-fold less computer memory. The reinforced SGD is also compared with SGD with fixed or adaptive momentum parameter and Nesterov's momentum, which shows that the proposed framework is able to reach a similar generalization accuracy with less computational costs. Overall, our method introduces stochastic memory into gradients, which plays an important role in understanding how gradient-based training algorithms can work and its relationship with generalization abilities of deep networks.

Unsupervised feature learning from finite data by message passing: discontinuous versus continuous phase transition

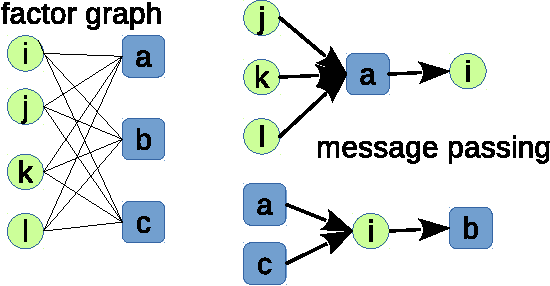
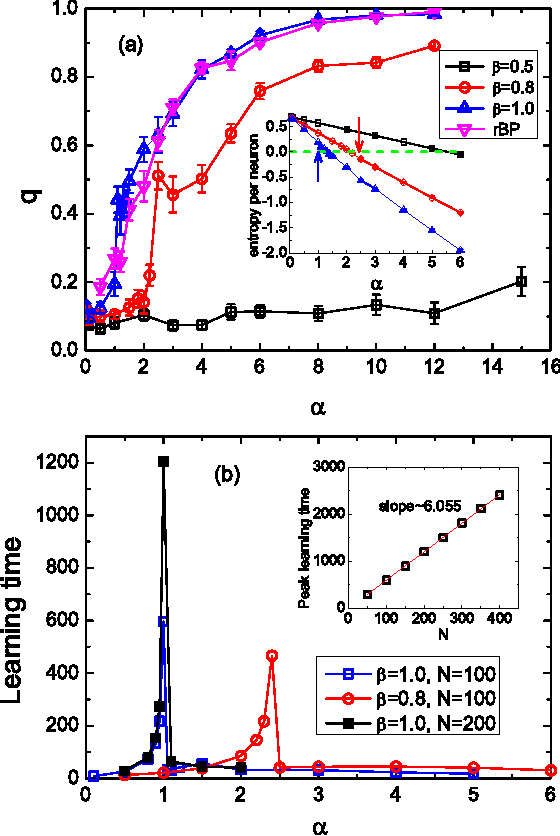
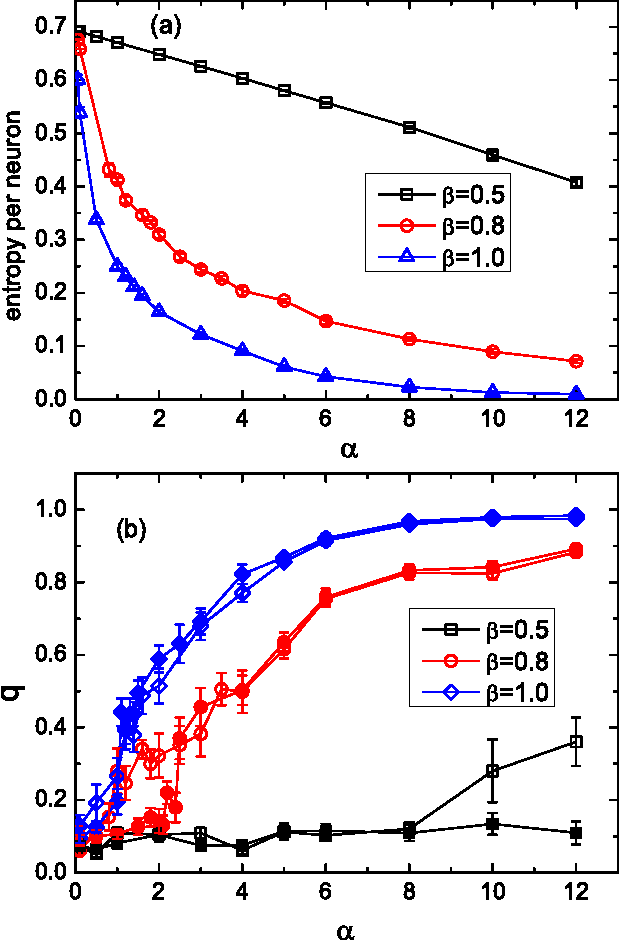
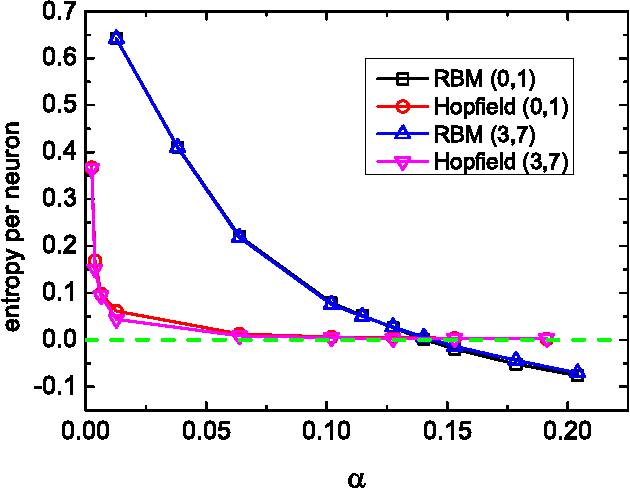
Unsupervised neural network learning extracts hidden features from unlabeled training data. This is used as a pretraining step for further supervised learning in deep networks. Hence, understanding unsupervised learning is of fundamental importance. Here, we study the unsupervised learning from a finite number of data, based on the restricted Boltzmann machine learning. Our study inspires an efficient message passing algorithm to infer the hidden feature, and estimate the entropy of candidate features consistent with the data. Our analysis reveals that the learning requires only a few data if the feature is salient and extensively many if the feature is weak. Moreover, the entropy of candidate features monotonically decreases with data size and becomes negative (i.e., entropy crisis) before the message passing becomes unstable, suggesting a discontinuous phase transition. In terms of convergence time of the message passing algorithm, the unsupervised learning exhibits an easy-hard-easy phenomenon as the training data size increases. All these properties are reproduced in an approximate Hopfield model, with an exception that the entropy crisis is absent, and only continuous phase transition is observed. This key difference is also confirmed in a handwritten digits dataset. This study deepens our understanding of unsupervised learning from a finite number of data, and may provide insights into its role in training deep networks.

Advanced Mean Field Theory of Restricted Boltzmann Machine

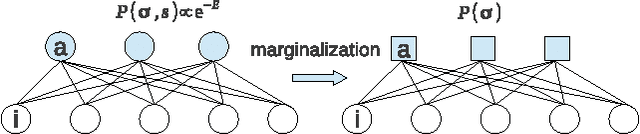
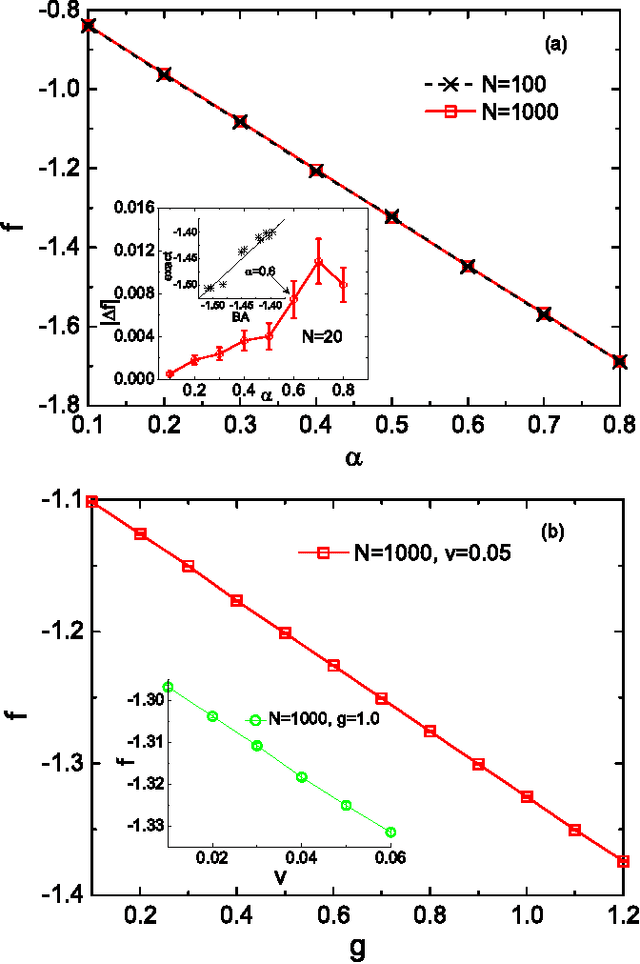
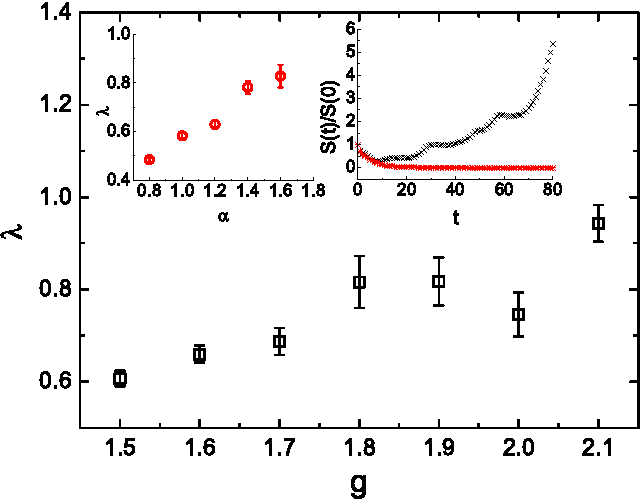
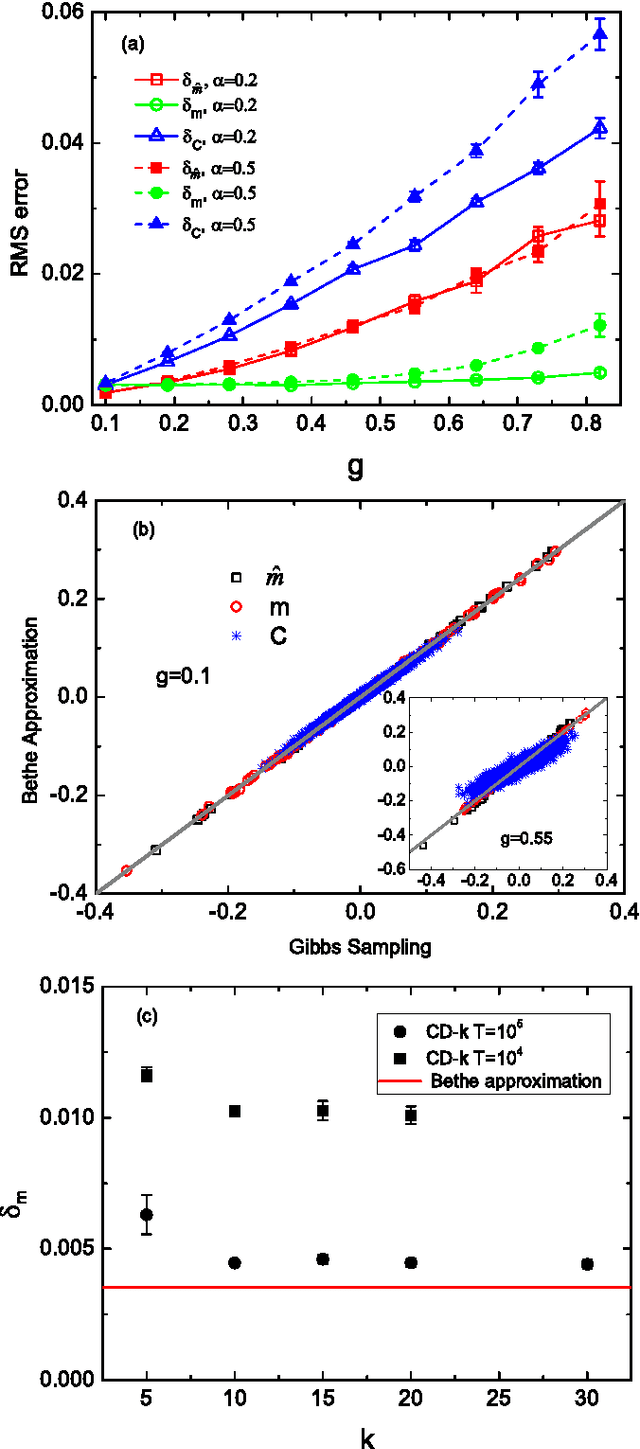
Learning in restricted Boltzmann machine is typically hard due to the computation of gradients of log-likelihood function. To describe the network state statistics of the restricted Boltzmann machine, we develop an advanced mean field theory based on the Bethe approximation. Our theory provides an efficient message passing based method that evaluates not only the partition function (free energy) but also its gradients without requiring statistical sampling. The results are compared with those obtained by the computationally expensive sampling based method.