On the achievability of blind source separation for high-dimensional nonlinear source mixtures

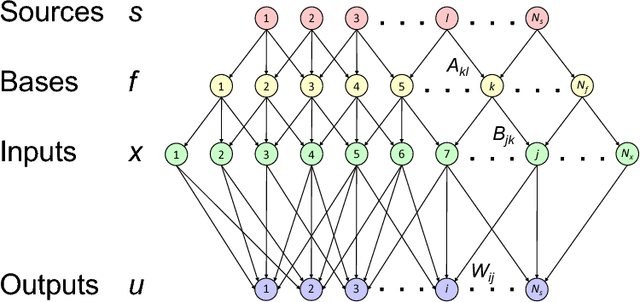
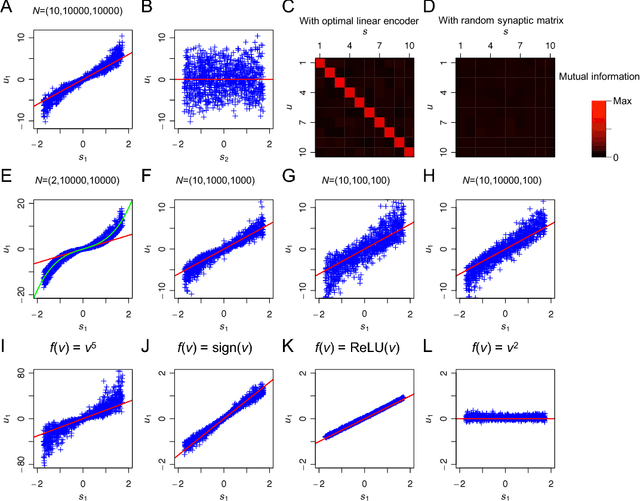
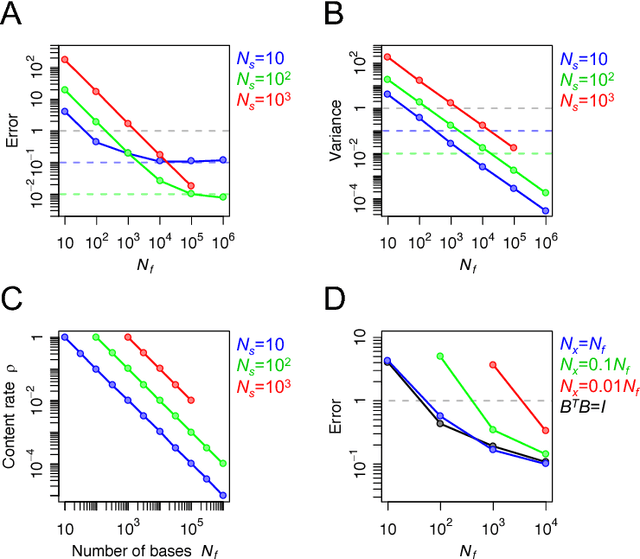
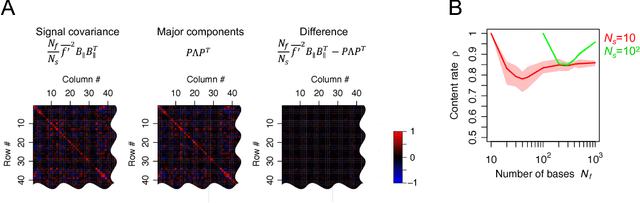
For many years, a combination of principal component analysis (PCA) and independent component analysis (ICA) has been used as a blind source separation (BSS) technique to separate hidden sources of natural data. However, it is unclear why these linear methods work well because most real-world data involve nonlinear mixtures of sources. We show that a cascade of PCA and ICA can solve this nonlinear BSS problem accurately as the variety of input signals increases. Specifically, we present two theorems that guarantee asymptotically zero-error BSS when sources are mixed by a feedforward network with two processing layers. Our first theorem analytically quantifies the performance of an optimal linear encoder that reconstructs independent sources. Zero-error is asymptotically reached when the number of sources is large and the numbers of inputs and nonlinear bases are large relative to the number of sources. The next question involves finding an optimal linear encoder without observing the underlying sources. Our second theorem guarantees that PCA can reliably extract all the subspace represented by the optimal linear encoder, so that a subsequent application of ICA can separate all sources. Thereby, for almost all nonlinear generative processes with sufficient variety, the cascade of PCA and ICA performs asymptotically zero-error BSS in an unsupervised manner. We analytically and numerically validate the theorems. These results highlight the utility of linear BSS techniques for accurately recovering nonlinearly mixed sources when observations are sufficiently diverse. We also discuss a possible biological BSS implementation.