Unsupervised feature learning from finite data by message passing: discontinuous versus continuous phase transition
Paper and Code
Nov 11, 2016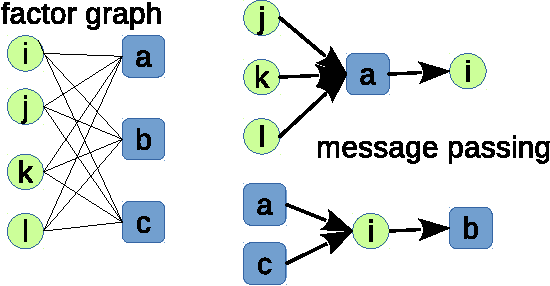
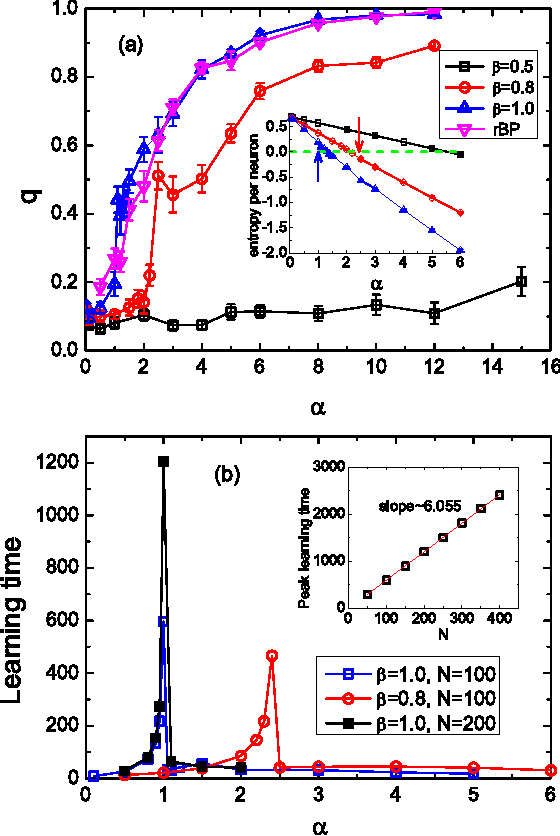
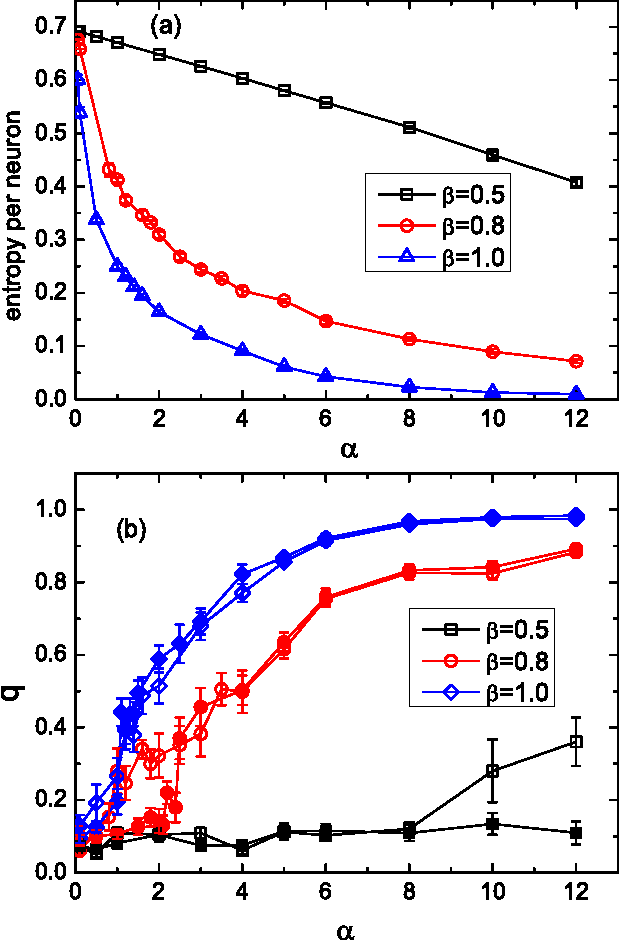
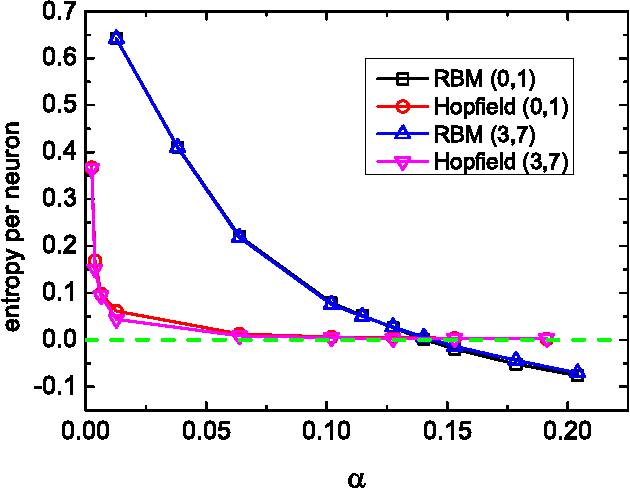
Unsupervised neural network learning extracts hidden features from unlabeled training data. This is used as a pretraining step for further supervised learning in deep networks. Hence, understanding unsupervised learning is of fundamental importance. Here, we study the unsupervised learning from a finite number of data, based on the restricted Boltzmann machine learning. Our study inspires an efficient message passing algorithm to infer the hidden feature, and estimate the entropy of candidate features consistent with the data. Our analysis reveals that the learning requires only a few data if the feature is salient and extensively many if the feature is weak. Moreover, the entropy of candidate features monotonically decreases with data size and becomes negative (i.e., entropy crisis) before the message passing becomes unstable, suggesting a discontinuous phase transition. In terms of convergence time of the message passing algorithm, the unsupervised learning exhibits an easy-hard-easy phenomenon as the training data size increases. All these properties are reproduced in an approximate Hopfield model, with an exception that the entropy crisis is absent, and only continuous phase transition is observed. This key difference is also confirmed in a handwritten digits dataset. This study deepens our understanding of unsupervised learning from a finite number of data, and may provide insights into its role in training deep networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge