Improving Methodologies for Agentic Evaluations Across Domains: Leakage of Sensitive Information, Fraud and Cybersecurity Threats

The rapid rise of autonomous AI systems and advancements in agent capabilities are introducing new risks due to reduced oversight of real-world interactions. Yet agent testing remains nascent and is still a developing science. As AI agents begin to be deployed globally, it is important that they handle different languages and cultures accurately and securely. To address this, participants from The International Network for Advanced AI Measurement, Evaluation and Science, including representatives from Singapore, Japan, Australia, Canada, the European Commission, France, Kenya, South Korea, and the United Kingdom have come together to align approaches to agentic evaluations. This is the third exercise, building on insights from two earlier joint testing exercises conducted by the Network in November 2024 and February 2025. The objective is to further refine best practices for testing advanced AI systems. The exercise was split into two strands: (1) common risks, including leakage of sensitive information and fraud, led by Singapore AISI; and (2) cybersecurity, led by UK AISI. A mix of open and closed-weight models were evaluated against tasks from various public agentic benchmarks. Given the nascency of agentic testing, our primary focus was on understanding methodological issues in conducting such tests, rather than examining test results or model capabilities. This collaboration marks an important step forward as participants work together to advance the science of agentic evaluations.

Improving Methodologies for LLM Evaluations Across Global Languages

As frontier AI models are deployed globally, it is essential that their behaviour remains safe and reliable across diverse linguistic and cultural contexts. To examine how current model safeguards hold up in such settings, participants from the International Network for Advanced AI Measurement, Evaluation and Science, including representatives from Singapore, Japan, Australia, Canada, the EU, France, Kenya, South Korea and the UK conducted a joint multilingual evaluation exercise. Led by Singapore AISI, two open-weight models were tested across ten languages spanning high and low resourced groups: Cantonese English, Farsi, French, Japanese, Korean, Kiswahili, Malay, Mandarin Chinese and Telugu. Over 6,000 newly translated prompts were evaluated across five harm categories (privacy, non-violent crime, violent crime, intellectual property and jailbreak robustness), using both LLM-as-a-judge and human annotation. The exercise shows how safety behaviours can vary across languages. These include differences in safeguard robustness across languages and harm types and variation in evaluator reliability (LLM-as-judge vs. human review). Further, it also generated methodological insights for improving multilingual safety evaluations, such as the need for culturally contextualised translations, stress-tested evaluator prompts and clearer human annotation guidelines. This work represents an initial step toward a shared framework for multilingual safety testing of advanced AI systems and calls for continued collaboration with the wider research community and industry.

Towards Human-Level Learning of Complex Physical Puzzles

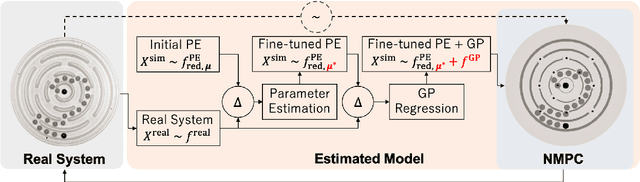
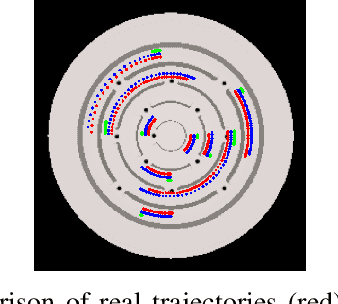
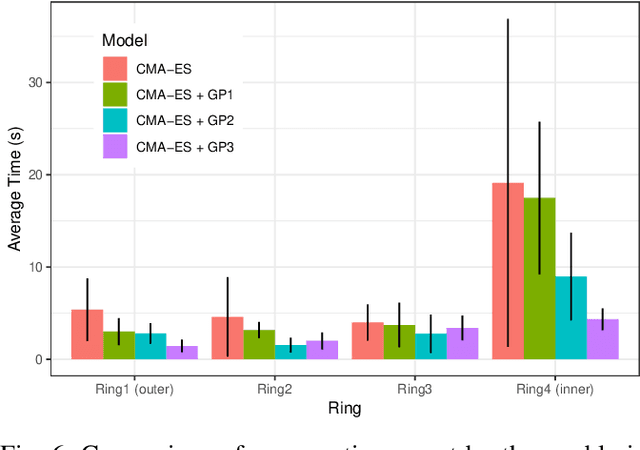
Humans quickly solve tasks in novel systems with complex dynamics, without requiring much interaction. While deep reinforcement learning algorithms have achieved tremendous success in many complex tasks, these algorithms need a large number of samples to learn meaningful policies. In this paper, we present a task for navigating a marble to the center of a circular maze. While this system is very intuitive and easy for humans to solve, it can be very difficult and inefficient for standard reinforcement learning algorithms to learn meaningful policies. We present a model that learns to move a marble in the complex environment within minutes of interacting with the real system. Learning consists of initializing a physics engine with parameters estimated using data from the real system. The error in the physics engine is then corrected using Gaussian process regression, which is used to model the residual between real observations and physics engine simulations. The physics engine equipped with the residual model is then used to control the marble in the maze environment using a model-predictive feedback over a receding horizon. We contrast the learning behavior against the time taken by humans to solve the problem to show comparable behavior. To the best of our knowledge, this is the first time that a hybrid model consisting of a full physics engine along with a statistical function approximator has been used to control a complex physical system in real-time using nonlinear model-predictive control (NMPC). Codes for the simulation environment can be downloaded here https://www.merl.com/research/license/CME . A video describing our method could be found here https://youtu.be/xaxNCXBovpc .