Lightning-Fast Dual-Layer Lossless Coding for Radiance Format High Dynamic Range Images

This paper proposes a fast dual-layer lossless coding for high dynamic range images (HDRIs) in the Radiance format. The coding, which consists of a base layer and a lossless enhancement layer, provides a standard dynamic range image (SDRI) without requiring an additional algorithm at the decoder and can losslessly decode the HDRI by adding the residual signals (residuals) between the HDRI and SDRI to the SDRI, if desired. To suppress the dynamic range of the residuals in the enhancement layer, the coding directly uses the mantissa and exponent information from the Radiance format. To further reduce the residual energy, each mantissa is modeled (estimated) as a linear function, i.e., a simple linear regression, of the encoded-decoded SDRI in each region with the same exponent. This is called simple linear regressive mantissa estimator. Experimental results show that, compared with existing methods, our coding reduces the average bitrate by approximately $1.57$-$6.68$ % and significantly reduces the average encoder implementation time by approximately $87.13$-$98.96$ %.

Edge-Aware Extended Star-Tetrix Transforms for CFA-Sampled Raw Camera Image Compression

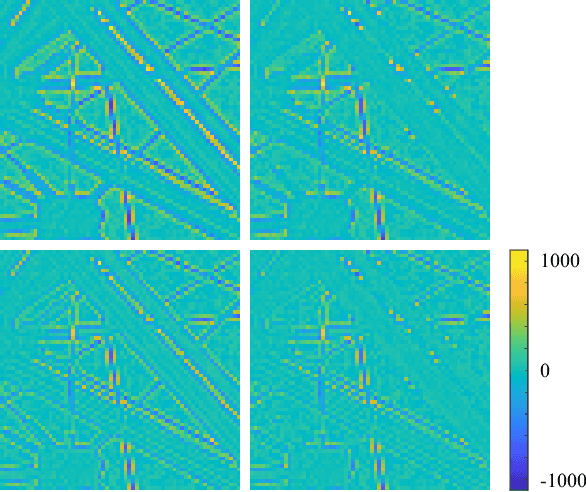
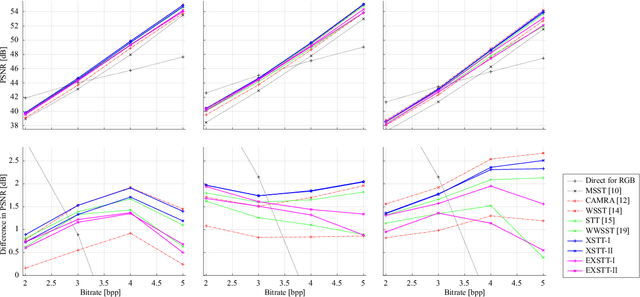
Codecs using spectral-spatial transforms efficiently compress raw camera images captured with a color filter array (CFA-sampled raw images) by changing their RGB color space into a decorrelated color space. This study describes two types of spectral-spatial transform, called extended Star-Tetrix transforms (XSTTs), and their edge-aware versions, called edge-aware XSTTs (EXSTTs), with no extra bits (side information) and little extra complexity. They are obtained by (i) extending the Star-Tetrix transform (STT), which is one of the latest spectral-spatial transforms, to a new version of our previously proposed wavelet-based spectral-spatial transform and a simpler version, (ii) considering that each 2-D predict step of the wavelet transform is a combination of two 1-D diagonal or horizontal-vertical transforms, and (iii) weighting the transforms along the edge directions in the images. Compared with XSTTs, the EXSTTs can decorrelate CFA-sampled raw images well: they reduce the difference in energy between the two green components by about $3.38$--$30.08$ \% for high-quality camera images and $8.97$--$14.47$ \% for mobile phone images. The experiments on JPEG 2000-based lossless and lossy compression of CFA-sampled raw images show better performance than conventional methods. For high-quality camera images, the XSTTs/EXSTTs produce results equal to or better than the conventional methods: especially for images with many edges, the type-I EXSTT improves them by about $0.03$--$0.19$ bpp in average lossless bitrate and the XSTTs improve them by about $0.16$--$0.96$ dB in average Bj\o ntegaard delta peak signal-to-noise ratio. For mobile phone images, our previous work perform the best, whereas the XSTTs/EXSTTs show similar trends to the case of high-quality camera images.

Regularity-constrained Fast Sine Transforms

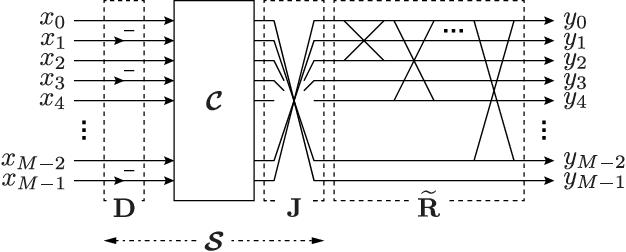
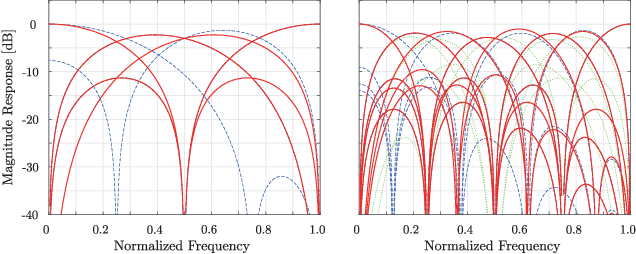
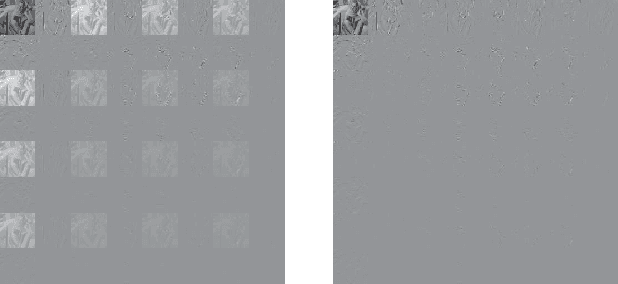
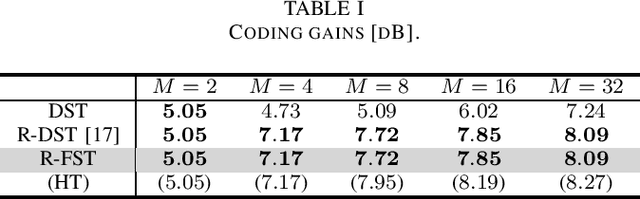
This letter proposes a fast implementation of the regularity-constrained discrete sine transform (R-DST). The original DST \textit{leaks} the lowest frequency (DC: direct current) components of signals into high frequency (AC: alternating current) subbands. This property is not desired in many applications, particularly image processing, since most of the frequency components in natural images concentrate in DC subband. The characteristic of filter banks whereby they do not leak DC components into the AC subbands is called \textit{regularity}. While an R-DST has been proposed, it has no fast implementation because of the singular value decomposition (SVD) in its internal algorithm. In contrast, the proposed regularity-constrained fast sine transform (R-FST) is obtained by just appending a regularity constraint matrix as a postprocessing of the original DST. When the DST size is $M\times M$ ($M=2^\ell$, $\ell\in\mathbb{N}_{\geq 1}$), the regularity constraint matrix is constructed from only $M/2-1$ rotation matrices with the angles derived from the output of the DST for the constant-valued signal (i.e., the DC signal). Since it does not require SVD, the computation is simpler and faster than the R-DST while keeping all of its beneficial properties. An image processing example shows that the R-FST has fine frequency selectivity with no DC leakage and higher coding gain than the original DST. Also, in the case of $M=8$, the R-FST saved approximately $0.126$ seconds in a 2-D transformation of $512\times 512$ signals compared with the R-DST because of fewer extra operations.

Directional Analytic Discrete Cosine Frames

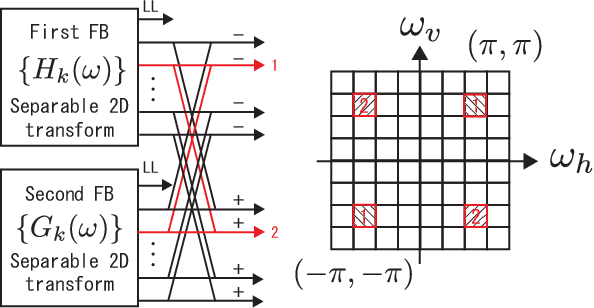
Block frames called directional analytic discrete cosine frames (DADCFs) are proposed for sparse image representation. In contrast to conventional overlapped frames, the proposed DADCFs require a reduced amount of 1) computational complexity, 2) memory usage, and 3) global memory access. These characteristics are strongly required for current high-resolution image processing. Specifically, we propose two DADCFs based on discrete cosine transform (DCT) and discrete sine transform (DST). The first DADCF is constructed from parallel separable transforms of DCT and DST, where the DST is permuted by row. The second DADCF is also designed based on DCT and DST, while the DST is customized to have no DC leakage property which is a desirable property for image processing. Both DADCFs have rich directional selectivity with slightly different characteristics each other and they can be implemented as non-overlapping block-based transforms, especially they form Parseval block frames with low transform redundancy. We perform experiments to evaluate our DADCFs and compare them with conventional directional block transforms in image recovery.