Auditory Attention Decoding without Spatial Information: A Diotic EEG Study

Auditory attention decoding (AAD) identifies the attended speech stream in multi-speaker environments by decoding brain signals such as electroencephalography (EEG). This technology is essential for realizing smart hearing aids that address the cocktail party problem and for facilitating objective audiometry systems. Existing AAD research mainly utilizes dichotic environments where different speech signals are presented to the left and right ears, enabling models to classify directional attention rather than speech content. However, this spatial reliance limits applicability to real-world scenarios, such as the "cocktail party" situation, where speakers overlap or move dynamically. To address this challenge, we propose an AAD framework for diotic environments where identical speech mixtures are presented to both ears, eliminating spatial cues. Our approach maps EEG and speech signals into a shared latent space using independent encoders. We extract speech features using wav2vec 2.0 and encode them with a 2-layer 1D convolutional neural network (CNN), while employing the BrainNetwork architecture for EEG encoding. The model identifies the attended speech by calculating the cosine similarity between EEG and speech representations. We evaluate our method on a diotic EEG dataset and achieve 72.70% accuracy, which is 22.58% higher than the state-of-the-art direction-based AAD method.

Graph Signal Denoising Using Regularization by Denoising and Its Parameter Estimation

In this paper, we propose an interpretable denoising method for graph signals using regularization by denoising (RED). RED is a technique developed for image restoration that uses an efficient (and sometimes black-box) denoiser in the regularization term of the optimization problem. By using RED, optimization problems can be designed with the explicit use of the denoiser, and the gradient of the regularization term can be easily computed under mild conditions. We adapt RED for denoising of graph signals beyond image processing. We show that many graph signal denoisers, including graph neural networks, theoretically or practically satisfy the conditions for RED. We also study the effectiveness of RED from a graph filter perspective. Furthermore, we propose supervised and unsupervised parameter estimation methods based on deep algorithm unrolling. These methods aim to enhance the algorithm applicability, particularly in the unsupervised setting. Denoising experiments for synthetic and real-world datasets show that our proposed method improves signal denoising accuracy in mean squared error compared to existing graph signal denoising methods.

Algorithm Unrolling-based Denoising of Multimodal Graph Signals

We propose a denoising method of multimodal graph signals by iteratively solving signal restoration and graph learning problems. Many complex-structured data, i.e., those on sensor networks, can capture multiple modalities at each measurement point, referred to as modalities. They are also assumed to have an underlying structure or correlations in modality as well as space. Such multimodal data are regarded as graph signals on a twofold graph and they are often corrupted by noise. Furthermore, their spatial/modality relationships are not always given a priori: We need to estimate twofold graphs during a denoising algorithm. In this paper, we consider a signal denoising method on twofold graphs, where graphs are learned simultaneously. We formulate an optimization problem for that and parameters in an iterative algorithm are learned from training data by unrolling the iteration with deep algorithm unrolling. Experimental results on synthetic and real-world data demonstrate that the proposed method outperforms existing model- and deep learning-based graph signal denoising methods.

Joint Graph Estimation and Signal Restoration for Robust Federated Learning

We propose a robust aggregation method for model parameters in federated learning (FL) under noisy communications. FL is a distributed machine learning paradigm in which a central server aggregates local model parameters from multiple clients. These parameters are often noisy and/or have missing values during data collection, training, and communication between the clients and server. This may cause a considerable drop in model accuracy. To address this issue, we learn a graph that represents pairwise relationships between model parameters of the clients during aggregation. We realize it with a joint problem of graph learning and signal (i.e., model parameters) restoration. The problem is formulated as a difference-of-convex (DC) optimization, which is efficiently solved via a proximal DC algorithm. Experimental results on MNIST and CIFAR-10 datasets show that the proposed method outperforms existing approaches by up to $2$--$5\%$ in classification accuracy under biased data distributions and noisy conditions.

Multiscale Graph Construction Using Non-local Cluster Features

This paper presents a multiscale graph construction method using both graph and signal features. Multiscale graph is a hierarchical representation of the graph, where a node at each level indicates a cluster in a finer resolution. To obtain the hierarchical clusters, existing methods often use graph clustering; however, they may ignore signal variations. As a result, these methods could fail to detect the clusters having similar features on nodes. In this paper, we consider graph and node-wise features simultaneously for multiscale clustering of a graph. With given clusters of the graph, the clusters are merged hierarchically in three steps: 1) Feature vectors in the clusters are extracted. 2) Similarities among cluster features are calculated using optimal transport. 3) A variable $k$-nearest neighbor graph (V$k$NNG) is constructed and graph spectral clustering is applied to the V$k$NNG to obtain clusters at a coarser scale. Additionally, the multiscale graph in this paper has \textit{non-local} characteristics: Nodes with similar features are merged even if they are spatially separated. In experiments on multiscale image and point cloud segmentation, we demonstrate the effectiveness of the proposed method.

Time-Varying Graph Signal Estimation among Multiple Sub-Networks

This paper presents an estimation method for time-varying graph signals among multiple sub-networks. In many sensor networks, signals observed are associated with nodes (i.e., sensors), and edges of the network represent the inter-node connectivity. For a large sensor network, measuring signal values at all nodes over time requires huge resources, particularly in terms of energy consumption. To alleviate the issue, we consider a scenario that a sub-network, i.e., cluster, from the whole network is extracted and an intra-cluster analysis is performed based on the statistics in the cluster. The statistics are then utilized to estimate signal values in another cluster. This leads to the requirement for transferring a set of parameters of the sub-network to the others, while the numbers of nodes in the clusters are typically different. In this paper, we propose a cooperative Kalman filter between two sub-networks. The proposed method alternately estimates signals in time between two sub-networks. We formulate a state-space model in the source cluster and transfer it to the target cluster on the basis of optimal transport. In the signal estimation experiments of synthetic and real-world signals, we validate the effectiveness of the proposed method.

Efficient Learning of Balanced Signed Graphs via Iterative Linear Programming

Signed graphs are equipped with both positive and negative edge weights, encoding pairwise correlations as well as anti-correlations in data. A balanced signed graph has no cycles of odd number of negative edges. Laplacian of a balanced signed graph has eigenvectors that map simply to ones in a similarity-transformed positive graph Laplacian, thus enabling reuse of well-studied spectral filters designed for positive graphs. We propose a fast method to learn a balanced signed graph Laplacian directly from data. Specifically, for each node $i$, to determine its polarity $\beta_i \in \{-1,1\}$ and edge weights $\{w_{i,j}\}_{j=1}^N$, we extend a sparse inverse covariance formulation based on linear programming (LP) called CLIME, by adding linear constraints to enforce ``consistent" signs of edge weights $\{w_{i,j}\}_{j=1}^N$ with the polarities of connected nodes -- i.e., positive/negative edges connect nodes of same/opposing polarities. For each LP, we adapt projections on convex set (POCS) to determine a suitable CLIME parameter $\rho > 0$ that guarantees LP feasibility. We solve the resulting LP via an off-the-shelf LP solver in $\mathcal{O}(N^{2.055})$. Experiments on synthetic and real-world datasets show that our balanced graph learning method outperforms competing methods and enables the use of spectral filters and graph convolutional networks (GCNs) designed for positive graphs on signed graphs.

Constructing an Interpretable Deep Denoiser by Unrolling Graph Laplacian Regularizer

An image denoiser can be used for a wide range of restoration problems via the Plug-and-Play (PnP) architecture. In this paper, we propose a general framework to build an interpretable graph-based deep denoiser (GDD) by unrolling a solution to a maximum a posteriori (MAP) problem equipped with a graph Laplacian regularizer (GLR) as signal prior. Leveraging a recent theorem showing that any (pseudo-)linear denoiser $\boldsymbol \Psi$, under mild conditions, can be mapped to a solution of a MAP denoising problem regularized using GLR, we first initialize a graph Laplacian matrix $\mathbf L$ via truncated Taylor Series Expansion (TSE) of $\boldsymbol \Psi^{-1}$. Then, we compute the MAP linear system solution by unrolling iterations of the conjugate gradient (CG) algorithm into a sequence of neural layers as a feed-forward network -- one that is amenable to parameter tuning. The resulting GDD network is "graph-interpretable", low in parameter count, and easy to initialize thanks to $\mathbf L$ derived from a known well-performing denoiser $\boldsymbol \Psi$. Experimental results show that GDD achieves competitive image denoising performance compared to competitors, but employing far fewer parameters, and is more robust to covariate shift.

Edge Sampling of Graphs: Graph Signal Processing Approach With Edge Smoothness

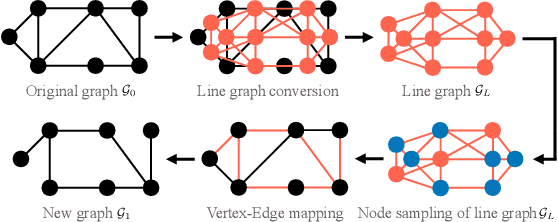
Finding important edges in a graph is a crucial problem for various research fields, such as network epidemics, signal processing, machine learning, and sensor networks. In this paper, we tackle the problem based on sampling theory on graphs. We convert the original graph to a line graph where its nodes and edges, respectively, represent the original edges and the connections between the edges. We then perform node sampling of the line graph based on the edge smoothness assumption: This process selects the most critical edges in the original graph. We present a general framework of edge sampling based on graph sampling theory and reveal a theoretical relationship between the degree of the original graph and the line graph. We also propose an acceleration method for edge sampling in the proposed framework by using the relationship between two types of Laplacian of the node and edge domains. Experimental results in synthetic and real-world graphs validate the effectiveness of our approach against some alternative edge selection methods.

Physics-Inspired Synthesized Underwater Image Dataset

This paper introduces the physics-inspired synthesized underwater image dataset (PHISWID), a dataset tailored for enhancing underwater image processing through physics-inspired image synthesis. Deep learning approaches to underwater image enhancement typically demand extensive datasets, yet acquiring paired clean and degraded underwater ones poses significant challenges. While several underwater image datasets have been proposed using physics-based synthesis, a publicly accessible collection has been lacking. Additionally, most underwater image synthesis approaches do not intend to reproduce atmospheric scenes, resulting in incomplete enhancement. PHISWID addresses this gap by offering a set of paired ground-truth (atmospheric) and synthetically degraded underwater images, showcasing not only color degradation but also the often-neglected effects of marine snow, a composite of organic matter and sand particles that considerably impairs underwater image clarity. The dataset applies these degradations to atmospheric RGB-D images, enhancing the dataset's realism and applicability. PHISWID is particularly valuable for training deep neural networks in a supervised learning setting and for objectively assessing image quality in benchmark analyses. Our results reveal that even a basic U-Net architecture, when trained with PHISWID, substantially outperforms existing methods in underwater image enhancement. We intend to release PHISWID publicly, contributing a significant resource to the advancement of underwater imaging technology.