Multiscale Graph Construction Using Non-local Cluster Features

This paper presents a multiscale graph construction method using both graph and signal features. Multiscale graph is a hierarchical representation of the graph, where a node at each level indicates a cluster in a finer resolution. To obtain the hierarchical clusters, existing methods often use graph clustering; however, they may ignore signal variations. As a result, these methods could fail to detect the clusters having similar features on nodes. In this paper, we consider graph and node-wise features simultaneously for multiscale clustering of a graph. With given clusters of the graph, the clusters are merged hierarchically in three steps: 1) Feature vectors in the clusters are extracted. 2) Similarities among cluster features are calculated using optimal transport. 3) A variable $k$-nearest neighbor graph (V$k$NNG) is constructed and graph spectral clustering is applied to the V$k$NNG to obtain clusters at a coarser scale. Additionally, the multiscale graph in this paper has \textit{non-local} characteristics: Nodes with similar features are merged even if they are spatially separated. In experiments on multiscale image and point cloud segmentation, we demonstrate the effectiveness of the proposed method.

Edge Sampling of Graphs: Graph Signal Processing Approach With Edge Smoothness

Finding important edges in a graph is a crucial problem for various research fields, such as network epidemics, signal processing, machine learning, and sensor networks. In this paper, we tackle the problem based on sampling theory on graphs. We convert the original graph to a line graph where its nodes and edges, respectively, represent the original edges and the connections between the edges. We then perform node sampling of the line graph based on the edge smoothness assumption: This process selects the most critical edges in the original graph. We present a general framework of edge sampling based on graph sampling theory and reveal a theoretical relationship between the degree of the original graph and the line graph. We also propose an acceleration method for edge sampling in the proposed framework by using the relationship between two types of Laplacian of the node and edge domains. Experimental results in synthetic and real-world graphs validate the effectiveness of our approach against some alternative edge selection methods.

Lossy Compression of Adjacency Matrices by Graph Filter Banks

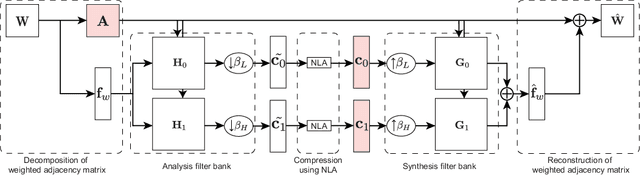
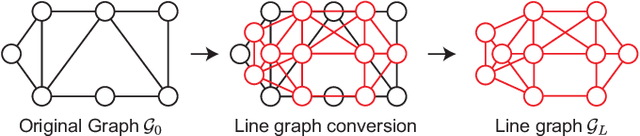
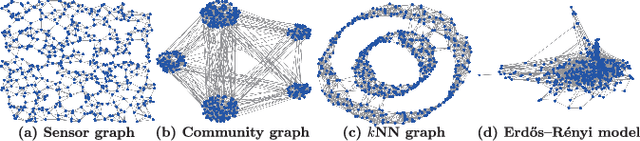
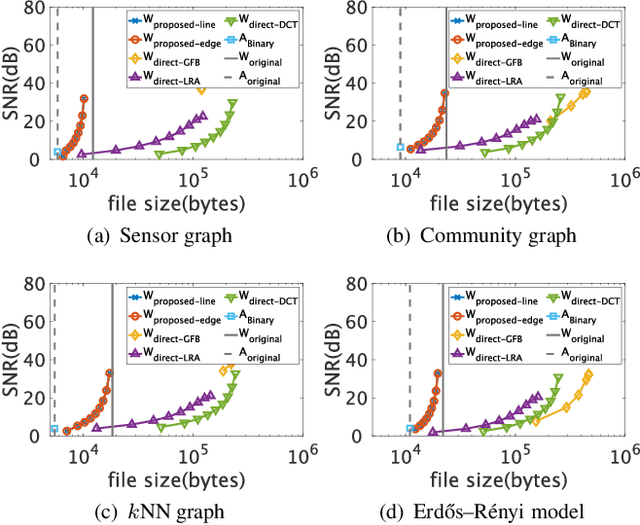
This paper proposes a compression framework for adjacency matrices of weighted graphs based on graph filter banks. Adjacency matrices are widely used mathematical representations of graphs and are used in various applications in signal processing, machine learning, and data mining. In many problems of interest, these adjacency matrices can be large, so efficient compression methods are crucial. In this paper, we propose a lossy compression of weighted adjacency matrices, where the binary adjacency information is encoded losslessly (so the topological information of the graph is preserved) while the edge weights are compressed lossily. For the edge weight compression, the target graph is converted into a line graph, whose nodes correspond to the edges of the original graph, and where the original edge weights are regarded as a graph signal on the line graph. We then transform the edge weights on the line graph with a graph filter bank for sparse representation. Experiments on synthetic data validate the effectiveness of the proposed method by comparing it with existing lossy matrix compression methods.