Directional Analytic Discrete Cosine Frames
Paper and Code
Dec 23, 2021


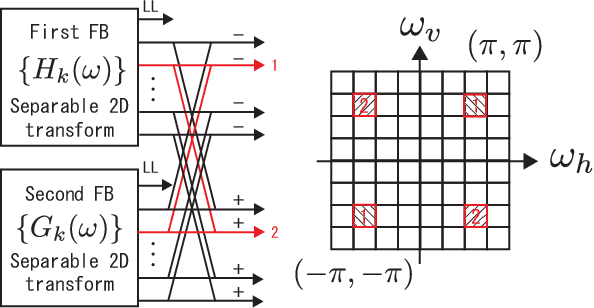
Block frames called directional analytic discrete cosine frames (DADCFs) are proposed for sparse image representation. In contrast to conventional overlapped frames, the proposed DADCFs require a reduced amount of 1) computational complexity, 2) memory usage, and 3) global memory access. These characteristics are strongly required for current high-resolution image processing. Specifically, we propose two DADCFs based on discrete cosine transform (DCT) and discrete sine transform (DST). The first DADCF is constructed from parallel separable transforms of DCT and DST, where the DST is permuted by row. The second DADCF is also designed based on DCT and DST, while the DST is customized to have no DC leakage property which is a desirable property for image processing. Both DADCFs have rich directional selectivity with slightly different characteristics each other and they can be implemented as non-overlapping block-based transforms, especially they form Parseval block frames with low transform redundancy. We perform experiments to evaluate our DADCFs and compare them with conventional directional block transforms in image recovery.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge