A Design of Denser-Graph-Frequency Graph Fourier Frames for Graph Signal Analysis

This paper introduces a design method for densergraph-frequency graph Fourier frames (DGFFs) to enhance graph signal processing and analysis. The graph Fourier transform (GFT) enables us to analyze graph signals in the graph spectral domain and facilitates various graph signal processing tasks, such as filtering, sampling and reconstruction, denoising, and so on. However, the conventional GFT faces two significant limitations. First, unlike the discrete Fourier transform and its variants (such as discrete cosine transforms), the graph frequencies of the derived graph Fourier basis (GFB) from a given graph tend to be unevenly distributed or localized, which leads to biased spectral analysis. Second, the GFB used in GFT does not provide an efficient sparse representation of graph signals compared to overcomplete systems like frames. To overcome these challenges, we propose adding oscillating vectors with intermediate graph frequencies between the original vectors in the GFB for both undirected and directed graphs, constructing GFFs with densergraph frequencies. The resulting DGFFs are expected to enable more accurate graph signal analysis. Furthermore, we propose a graph filtering method based on the DGFFs. In experiments, we apply the DGFFs to practical applications such as graph signal recovery, demonstrating superior performance compared to existing GFBs.

Regularity-constrained Fast Sine Transforms

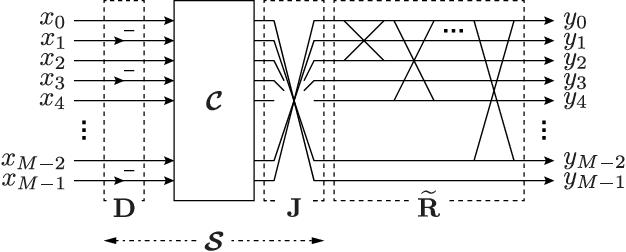
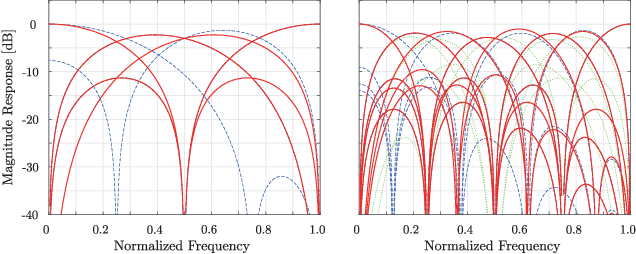
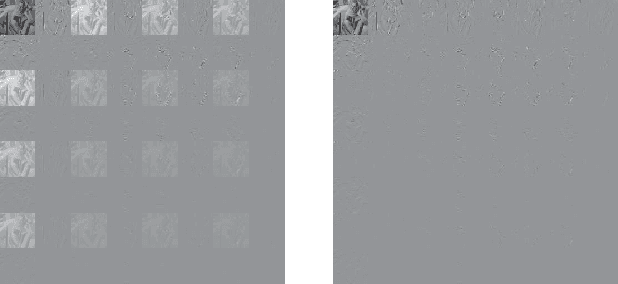
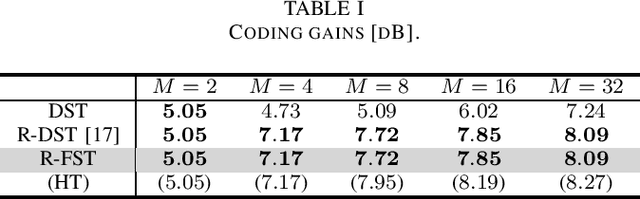
This letter proposes a fast implementation of the regularity-constrained discrete sine transform (R-DST). The original DST \textit{leaks} the lowest frequency (DC: direct current) components of signals into high frequency (AC: alternating current) subbands. This property is not desired in many applications, particularly image processing, since most of the frequency components in natural images concentrate in DC subband. The characteristic of filter banks whereby they do not leak DC components into the AC subbands is called \textit{regularity}. While an R-DST has been proposed, it has no fast implementation because of the singular value decomposition (SVD) in its internal algorithm. In contrast, the proposed regularity-constrained fast sine transform (R-FST) is obtained by just appending a regularity constraint matrix as a postprocessing of the original DST. When the DST size is $M\times M$ ($M=2^\ell$, $\ell\in\mathbb{N}_{\geq 1}$), the regularity constraint matrix is constructed from only $M/2-1$ rotation matrices with the angles derived from the output of the DST for the constant-valued signal (i.e., the DC signal). Since it does not require SVD, the computation is simpler and faster than the R-DST while keeping all of its beneficial properties. An image processing example shows that the R-FST has fine frequency selectivity with no DC leakage and higher coding gain than the original DST. Also, in the case of $M=8$, the R-FST saved approximately $0.126$ seconds in a 2-D transformation of $512\times 512$ signals compared with the R-DST because of fewer extra operations.

Directional Analytic Discrete Cosine Frames

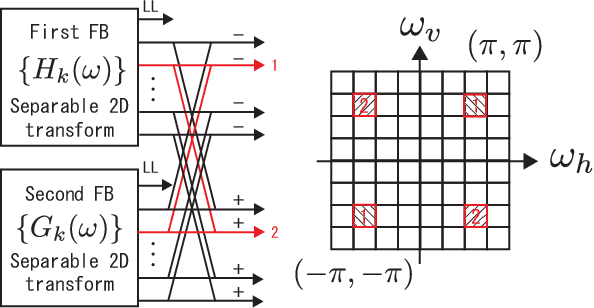
Block frames called directional analytic discrete cosine frames (DADCFs) are proposed for sparse image representation. In contrast to conventional overlapped frames, the proposed DADCFs require a reduced amount of 1) computational complexity, 2) memory usage, and 3) global memory access. These characteristics are strongly required for current high-resolution image processing. Specifically, we propose two DADCFs based on discrete cosine transform (DCT) and discrete sine transform (DST). The first DADCF is constructed from parallel separable transforms of DCT and DST, where the DST is permuted by row. The second DADCF is also designed based on DCT and DST, while the DST is customized to have no DC leakage property which is a desirable property for image processing. Both DADCFs have rich directional selectivity with slightly different characteristics each other and they can be implemented as non-overlapping block-based transforms, especially they form Parseval block frames with low transform redundancy. We perform experiments to evaluate our DADCFs and compare them with conventional directional block transforms in image recovery.