Regularity-constrained Fast Sine Transforms

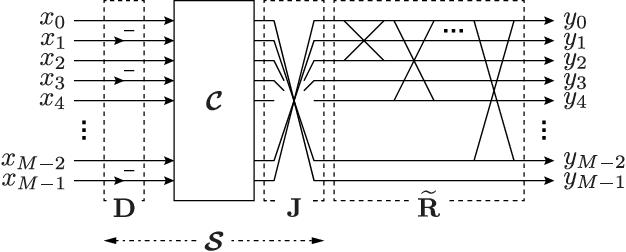
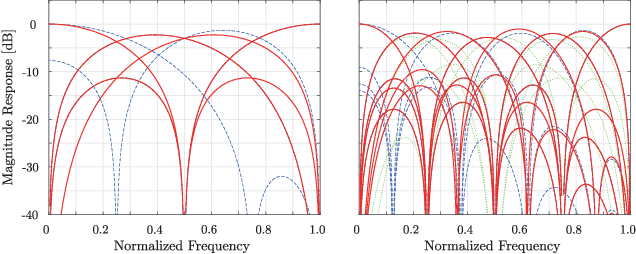
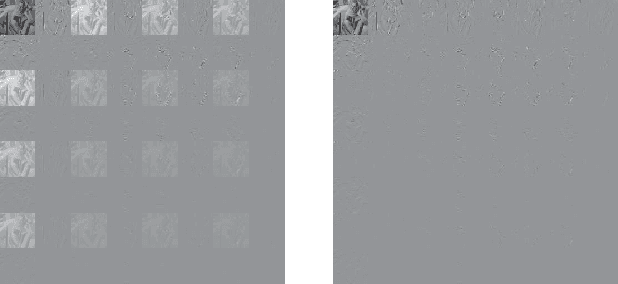
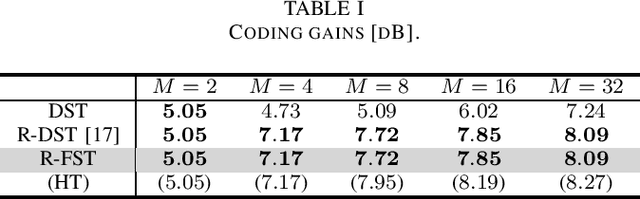
This letter proposes a fast implementation of the regularity-constrained discrete sine transform (R-DST). The original DST \textit{leaks} the lowest frequency (DC: direct current) components of signals into high frequency (AC: alternating current) subbands. This property is not desired in many applications, particularly image processing, since most of the frequency components in natural images concentrate in DC subband. The characteristic of filter banks whereby they do not leak DC components into the AC subbands is called \textit{regularity}. While an R-DST has been proposed, it has no fast implementation because of the singular value decomposition (SVD) in its internal algorithm. In contrast, the proposed regularity-constrained fast sine transform (R-FST) is obtained by just appending a regularity constraint matrix as a postprocessing of the original DST. When the DST size is $M\times M$ ($M=2^\ell$, $\ell\in\mathbb{N}_{\geq 1}$), the regularity constraint matrix is constructed from only $M/2-1$ rotation matrices with the angles derived from the output of the DST for the constant-valued signal (i.e., the DC signal). Since it does not require SVD, the computation is simpler and faster than the R-DST while keeping all of its beneficial properties. An image processing example shows that the R-FST has fine frequency selectivity with no DC leakage and higher coding gain than the original DST. Also, in the case of $M=8$, the R-FST saved approximately $0.126$ seconds in a 2-D transformation of $512\times 512$ signals compared with the R-DST because of fewer extra operations.