New Methods & Metrics for LFQA tasks

Long-form question answering (LFQA) tasks require retrieving the documents pertinent to a query, using them to form a paragraph-length answer. Despite considerable progress in LFQA modeling, fundamental issues impede its progress: i) train/validation/test dataset overlap, ii) absence of automatic metrics and iii) generated answers not being "grounded" in retrieved documents. This work addresses every one these critical bottlenecks, contributing natural language inference/generation (NLI/NLG) methods and metrics that make significant strides to their alleviation.

Discretized Bottleneck in VAE: Posterior-Collapse-Free Sequence-to-Sequence Learning

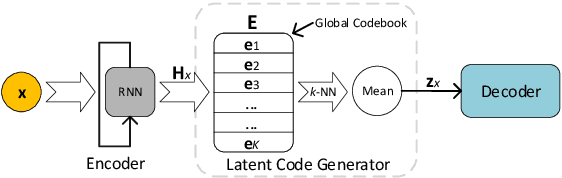
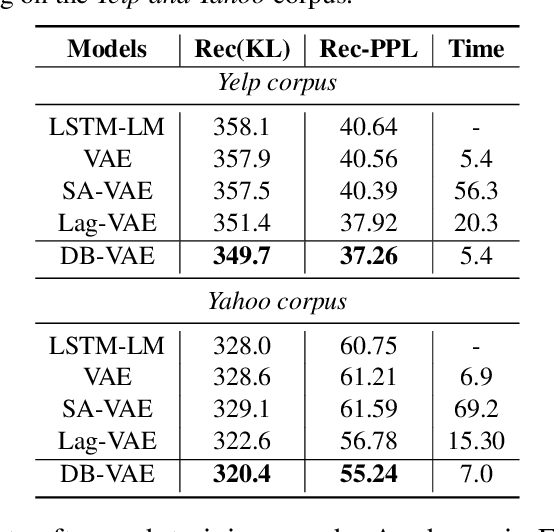
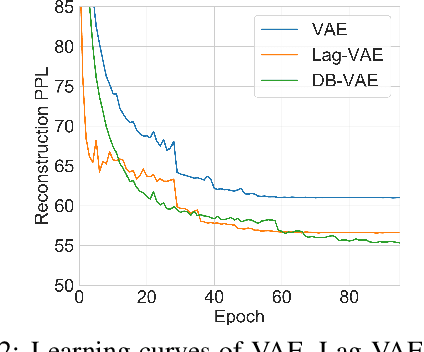
Variational autoencoders (VAEs) are important tools in end-to-end representation learning. VAEs can capture complex data distributions and have been applied extensively in many natural-language-processing (NLP) tasks. However, a common pitfall in sequence-to-sequence learning with VAEs is the posterior-collapse issue in latent space, wherein the model tends to ignore latent variables when a strong auto-regressive decoder is implemented. In this paper, we propose a principled approach to eliminate this issue by applying a discretized bottleneck in the latent space. Specifically, we impose a shared discrete latent space where each input is learned to choose a combination of shared latent atoms as its latent representation. Compared with VAEs employing continuous latent variables, our model endows more promising capability in modeling underlying semantics of discrete sequences and can thus provide more interpretative latent structures. Empirically, we demonstrate the efficiency and effectiveness of our model on a broad range of tasks, including language modeling, unaligned text style transfer, dialog response generation, and neural machine translation.

Learning Manifolds from Non-stationary Streaming Data

Streaming adaptations of manifold learning based dimensionality reduction methods, such as Isomap, typically assume that the underlying data distribution is stationary. Such methods are not equipped to detect or handle sudden changes or gradual drifts in the distribution generating the stream. We prove that a Gaussian Process Regression (GPR) model that uses a manifold-specific kernel function and is trained on an initial batch of sufficient size, can closely approximate the state-of-art streaming Isomap algorithm. The predictive variance obtained from the GPR prediction is then shown to be an effective detector of changes in the underlying data distribution. Results on several synthetic and real data sets show that the resulting algorithm can effectively learns lower dimensional representation of high dimensional data in a streaming setting, while identify shifts in the generative distribution.

S-Isomap++: Multi Manifold Learning from Streaming Data

Manifold learning based methods have been widely used for non-linear dimensionality reduction (NLDR). However, in many practical settings, the need to process streaming data is a challenge for such methods, owing to the high computational complexity involved. Moreover, most methods operate under the assumption that the input data is sampled from a single manifold, embedded in a high dimensional space. We propose a method for streaming NLDR when the observed data is either sampled from multiple manifolds or irregularly sampled from a single manifold. We show that existing NLDR methods, such as Isomap, fail in such situations, primarily because they rely on smoothness and continuity of the underlying manifold, which is violated in the scenarios explored in this paper. However, the proposed algorithm is able to learn effectively in presence of multiple, and potentially intersecting, manifolds, while allowing for the input data to arrive as a massive stream.

Error Metrics for Learning Reliable Manifolds from Streaming Data

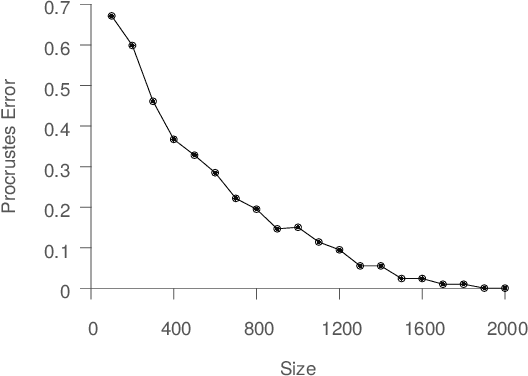
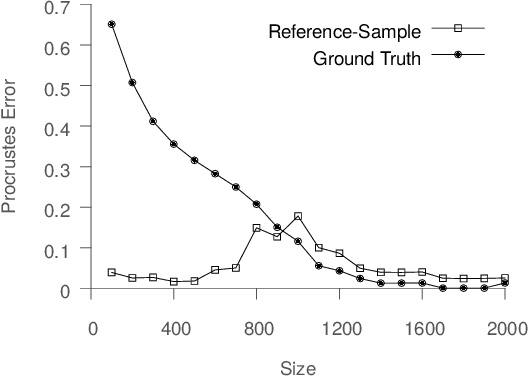
Spectral dimensionality reduction is frequently used to identify low-dimensional structure in high-dimensional data. However, learning manifolds, especially from the streaming data, is computationally and memory expensive. In this paper, we argue that a stable manifold can be learned using only a fraction of the stream, and the remaining stream can be mapped to the manifold in a significantly less costly manner. Identifying the transition point at which the manifold is stable is the key step. We present error metrics that allow us to identify the transition point for a given stream by quantitatively assessing the quality of a manifold learned using Isomap. We further propose an efficient mapping algorithm, called S-Isomap, that can be used to map new samples onto the stable manifold. We describe experiments on a variety of data sets that show that the proposed approach is computationally efficient without sacrificing accuracy.