Scalable Manifold Learning for Big Data with Apache Spark

Non-linear spectral dimensionality reduction methods, such as Isomap, remain important technique for learning manifolds. However, due to computational complexity, exact manifold learning using Isomap is currently impossible from large-scale data. In this paper, we propose a distributed memory framework implementing end-to-end exact Isomap under Apache Spark model. We show how each critical step of the Isomap algorithm can be efficiently realized using basic Spark model, without the need to provision data in the secondary storage. We show how the entire method can be implemented using PySpark, offloading compute intensive linear algebra routines to BLAS. Through experimental results, we demonstrate excellent scalability of our method, and we show that it can process datasets orders of magnitude larger than what is currently possible, using a 25-node parallel~cluster.

Entropy-Isomap: Manifold Learning for High-dimensional Dynamic Processes

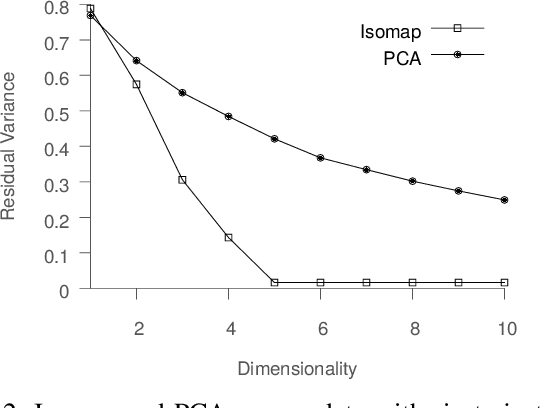
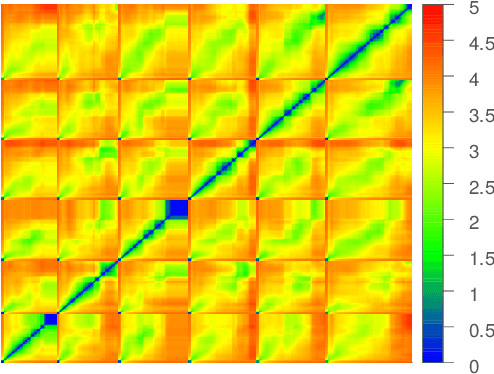
Scientific and engineering processes deliver massive high-dimensional data sets that are generated as non-linear transformations of an initial state and few process parameters. Mapping such data to a low-dimensional manifold facilitates better understanding of the underlying processes, and enables their optimization. In this paper, we first show that off-the-shelf non-linear spectral dimensionality reduction methods, e.g., Isomap, fail for such data, primarily due to the presence of strong temporal correlations. Then, we propose a novel method, Entropy-Isomap, to address the issue. The proposed method is successfully applied to large data describing a fabrication process of organic materials. The resulting low-dimensional representation correctly captures process control variables, allows for low-dimensional visualization of the material morphology evolution, and provides key insights to improve the process.

Error Metrics for Learning Reliable Manifolds from Streaming Data

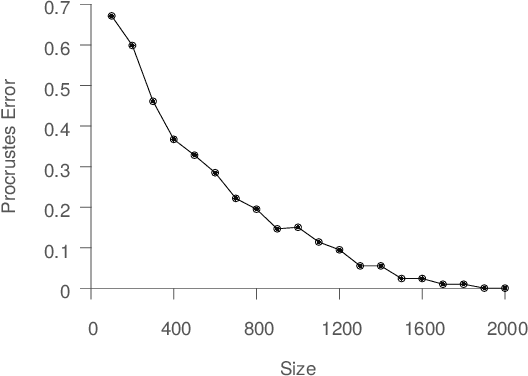
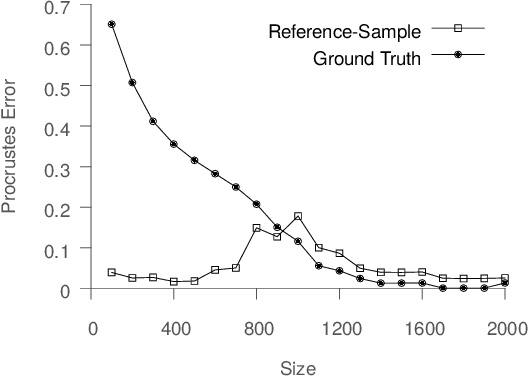
Spectral dimensionality reduction is frequently used to identify low-dimensional structure in high-dimensional data. However, learning manifolds, especially from the streaming data, is computationally and memory expensive. In this paper, we argue that a stable manifold can be learned using only a fraction of the stream, and the remaining stream can be mapped to the manifold in a significantly less costly manner. Identifying the transition point at which the manifold is stable is the key step. We present error metrics that allow us to identify the transition point for a given stream by quantitatively assessing the quality of a manifold learned using Isomap. We further propose an efficient mapping algorithm, called S-Isomap, that can be used to map new samples onto the stable manifold. We describe experiments on a variety of data sets that show that the proposed approach is computationally efficient without sacrificing accuracy.