Causal machine learning for heterogeneous treatment effects in the presence of missing outcome data

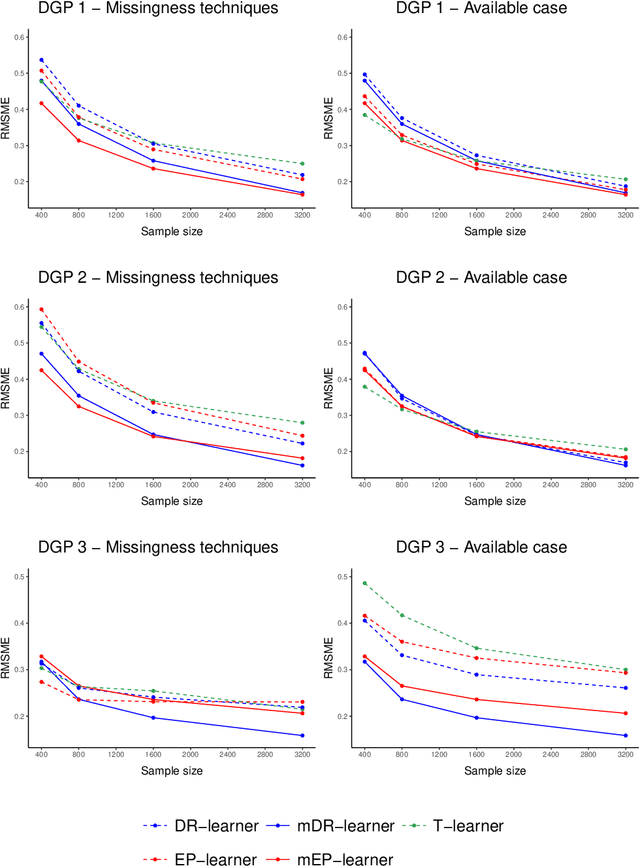
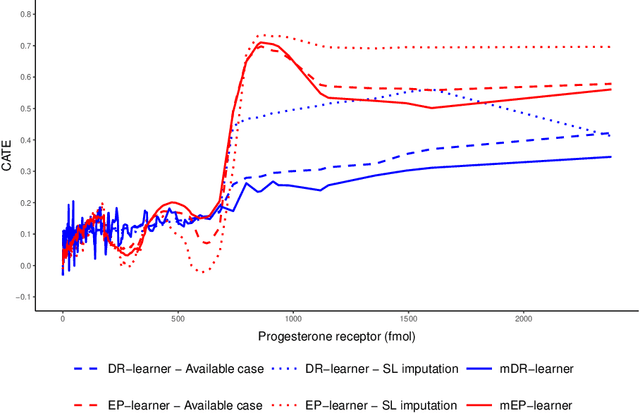
When estimating heterogeneous treatment effects, missing outcome data can complicate treatment effect estimation, causing certain subgroups of the population to be poorly represented. In this work, we discuss this commonly overlooked problem and consider the impact that missing at random (MAR) outcome data has on causal machine learning estimators for the conditional average treatment effect (CATE). We then propose two de-biased machine learning estimators for the CATE, the mDR-learner and mEP-learner, which address the issue of under-representation by integrating inverse probability of censoring weights into the DR-learner and EP-learner respectively. We show that under reasonable conditions, these estimators are oracle efficient, and illustrate their favorable performance through simulated data settings, comparing them to existing CATE estimators, including comparison to estimators which use common missing data techniques. Guidance on the implementation of these estimators is provided and we present an example of their application using the ACTG175 trial, exploring treatment effect heterogeneity when comparing Zidovudine mono-therapy against alternative antiretroviral therapies among HIV-1-infected individuals.

Debiasing Synthetic Data Generated by Deep Generative Models

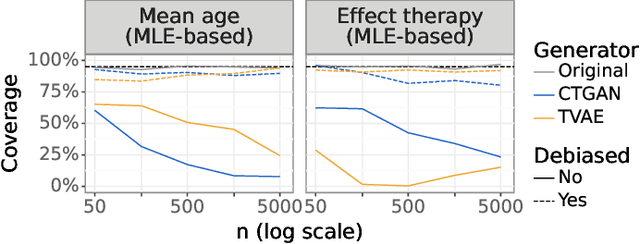
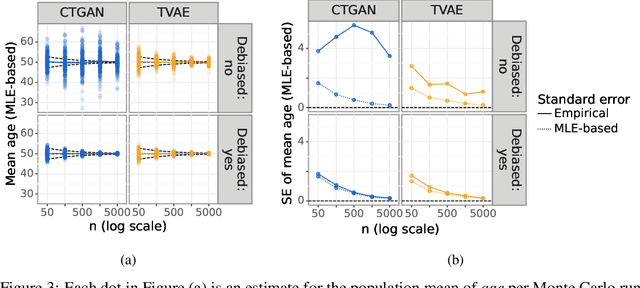
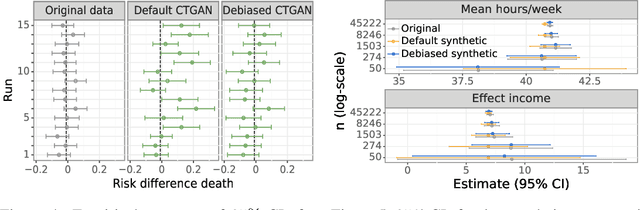
While synthetic data hold great promise for privacy protection, their statistical analysis poses significant challenges that necessitate innovative solutions. The use of deep generative models (DGMs) for synthetic data generation is known to induce considerable bias and imprecision into synthetic data analyses, compromising their inferential utility as opposed to original data analyses. This bias and uncertainty can be substantial enough to impede statistical convergence rates, even in seemingly straightforward analyses like mean calculation. The standard errors of such estimators then exhibit slower shrinkage with sample size than the typical 1 over root-$n$ rate. This complicates fundamental calculations like p-values and confidence intervals, with no straightforward remedy currently available. In response to these challenges, we propose a new strategy that targets synthetic data created by DGMs for specific data analyses. Drawing insights from debiased and targeted machine learning, our approach accounts for biases, enhances convergence rates, and facilitates the calculation of estimators with easily approximated large sample variances. We exemplify our proposal through a simulation study on toy data and two case studies on real-world data, highlighting the importance of tailoring DGMs for targeted data analysis. This debiasing strategy contributes to advancing the reliability and applicability of synthetic data in statistical inference.

Synthetic Data: Can We Trust Statistical Estimators?

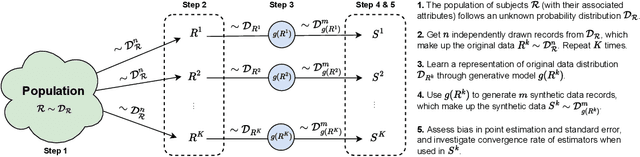
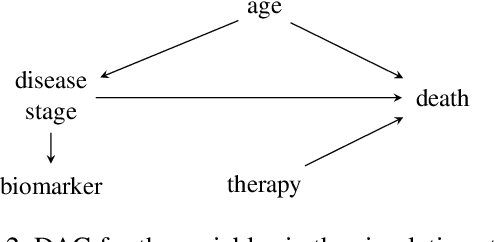
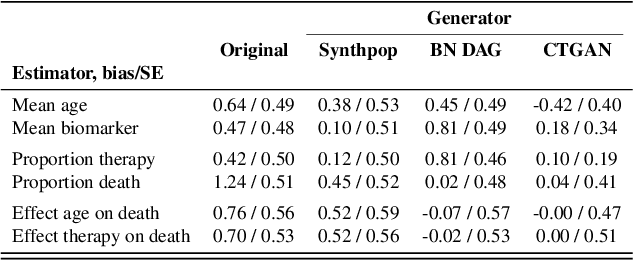
The increasing interest in data sharing makes synthetic data appealing. However, the analysis of synthetic data raises a unique set of methodological challenges. In this work, we highlight the importance of inferential utility and provide empirical evidence against naive inference from synthetic data (that handles these as if they were really observed). We argue that the rate of false-positive findings (type 1 error) will be unacceptably high, even when the estimates are unbiased. One of the reasons is the underestimation of the true standard error, which may even progressively increase with larger sample sizes due to slower convergence. This is especially problematic for deep generative models. Before publishing synthetic data, it is essential to develop statistical inference tools for such data.

Assumption-lean inference for generalised linear model parameters

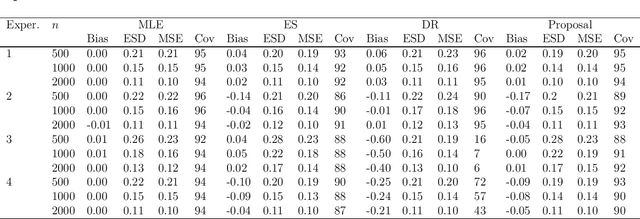
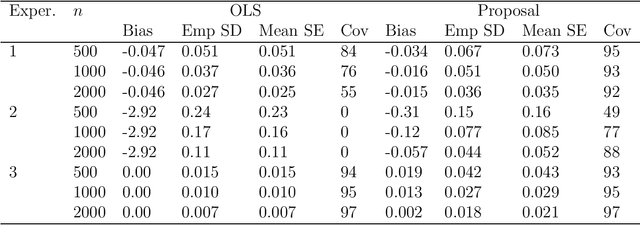
Inference for the parameters indexing generalised linear models is routinely based on the assumption that the model is correct and a priori specified. This is unsatisfactory because the chosen model is usually the result of a data-adaptive model selection process, which may induce excess uncertainty that is not usually acknowledged. Moreover, the assumptions encoded in the chosen model rarely represent some a priori known, ground truth, making standard inferences prone to bias, but also failing to give a pure reflection of the information that is contained in the data. Inspired by developments on assumption-free inference for so-called projection parameters, we here propose novel nonparametric definitions of main effect estimands and effect modification estimands. These reduce to standard main effect and effect modification parameters in generalised linear models when these models are correctly specified, but have the advantage that they continue to capture respectively the primary (conditional) association between two variables, or the degree to which two variables interact (in a statistical sense) in their effect on outcome, even when these models are misspecified. We achieve an assumption-lean inference for these estimands (and thus for the underlying regression parameters) by deriving their influence curve under the nonparametric model and invoking flexible data-adaptive (e.g., machine learning) procedures.