The Harmonic Exponential Filter for Nonparametric Estimation on Motion Groups

Bayesian estimation is a vital tool in robotics as it allows systems to update the belief of the robot state using incomplete information from noisy sensors. To render the state estimation problem tractable, many systems assume that the motion and measurement noise, as well as the state distribution, are all unimodal and Gaussian. However, there are numerous scenarios and systems that do not comply with these assumptions. Existing non-parametric filters that are used to model multimodal distributions have drawbacks that limit their ability to represent a diverse set of distributions. In this paper, we introduce a novel approach to nonparametric Bayesian filtering to cope with multimodal distributions using harmonic exponential distributions. This approach leverages two key insights of harmonic exponential distributions: a) the product of two distributions can be expressed as the element-wise addition of their log-likelihood Fourier coefficients, and b) the convolution of two distributions can be efficiently computed as the tensor product of their Fourier coefficients. These observations enable the development of an efficient and exact solution to the Bayes filter up to the band limit of a Fourier transform. We demonstrate our filter's superior performance compared with established nonparametric filtering methods across a range of simulated and real-world localization tasks.

Sparse Bayesian Inference for Dense Semantic Mapping

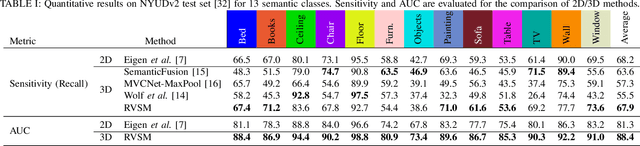
Despite impressive advances in simultaneous localization and mapping, dense robotic mapping remains challenging due to its inherent nature of being a high-dimensional inference problem. In this paper, we propose a dense semantic robotic mapping technique that exploits sparse Bayesian models, in particular, the relevance vector machine, for high-dimensional sequential inference. The technique is based on the principle of automatic relevance determination and produces sparse models that use a small subset of the original dense training set as the dominant basis. The resulting map posterior is continuous, and queries can be made efficiently at any resolution. Moreover, the technique has probabilistic outputs per semantic class through Bayesian inference. We evaluate the proposed relevance vector semantic map using publicly available benchmark datasets, NYU Depth V2 and KITTI; and the results show promising improvements over the state-of-the-art techniques.

Gaussian Processes Semantic Map Representation

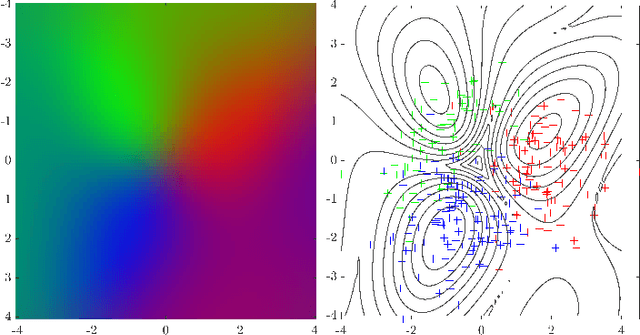
In this paper, we develop a high-dimensional map building technique that incorporates raw pixelated semantic measurements into the map representation. The proposed technique uses Gaussian Processes (GPs) multi-class classification for map inference and is the natural extension of GP occupancy maps from binary to multi-class form. The technique exploits the continuous property of GPs and, as a result, the map can be inferred with any resolution. In addition, the proposed GP Semantic Map (GPSM) learns the structural and semantic correlation from measurements rather than resorting to assumptions, and can flexibly learn the spatial correlation as well as any additional non-spatial correlation between map points. We extend the OctoMap to Semantic OctoMap representation and compare with the GPSM mapping performance using NYU Depth V2 dataset. Evaluations of the proposed technique on multiple partially labeled RGBD scans and labels from noisy image segmentation show that the GP semantic map can handle sparse measurements, missing labels in the point cloud, as well as noise corrupted labels.