Distributed Multi-robot Source Seeking in Unknown Environments with Unknown Number of Sources

We introduce a novel distributed source seeking framework, DIAS, designed for multi-robot systems in scenarios where the number of sources is unknown and potentially exceeds the number of robots. Traditional robotic source seeking methods typically focused on directing each robot to a specific strong source and may fall short in comprehensively identifying all potential sources. DIAS addresses this gap by introducing a hybrid controller that identifies the presence of sources and then alternates between exploration for data gathering and exploitation for guiding robots to identified sources. It further enhances search efficiency by dividing the environment into Voronoi cells and approximating source density functions based on Gaussian process regression. Additionally, DIAS can be integrated with existing source seeking algorithms. We compare DIAS with existing algorithms, including DoSS and GMES in simulated gas leakage scenarios where the number of sources outnumbers or is equal to the number of robots. The numerical results show that DIAS outperforms the baseline methods in both the efficiency of source identification by the robots and the accuracy of the estimated environmental density function.

DyPNIPP: Predicting Environment Dynamics for RL-based Robust Informative Path Planning

Informative path planning (IPP) is an important planning paradigm for various real-world robotic applications such as environment monitoring. IPP involves planning a path that can learn an accurate belief of the quantity of interest, while adhering to planning constraints. Traditional IPP methods typically require high computation time during execution, giving rise to reinforcement learning (RL) based IPP methods. However, the existing RL-based methods do not consider spatio-temporal environments which involve their own challenges due to variations in environment characteristics. In this paper, we propose DyPNIPP, a robust RL-based IPP framework, designed to operate effectively across spatio-temporal environments with varying dynamics. To achieve this, DyPNIPP incorporates domain randomization to train the agent across diverse environments and introduces a dynamics prediction model to capture and adapt the agent actions to specific environment dynamics. Our extensive experiments in a wildfire environment demonstrate that DyPNIPP outperforms existing RL-based IPP algorithms by significantly improving robustness and performing across diverse environment conditions.

OffRIPP: Offline RL-based Informative Path Planning

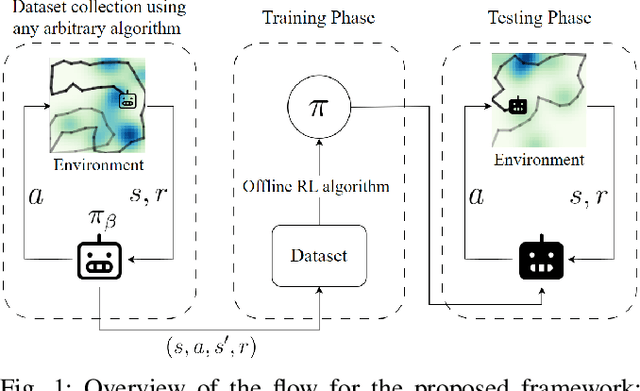
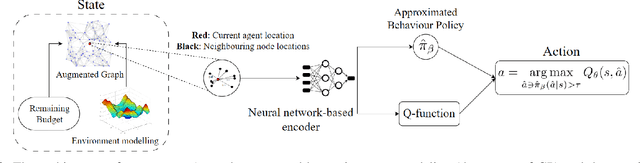
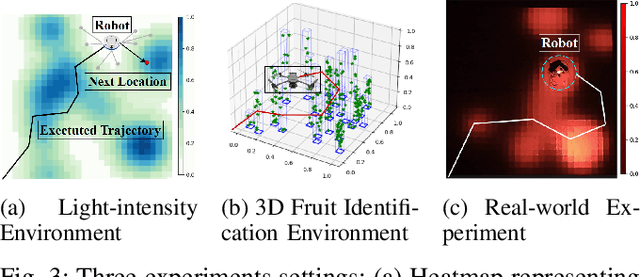
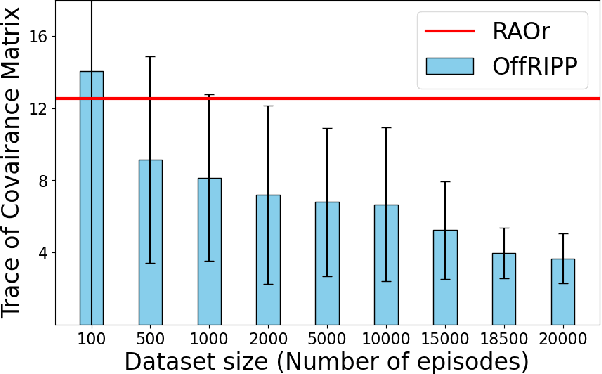
Informative path planning (IPP) is a crucial task in robotics, where agents must design paths to gather valuable information about a target environment while adhering to resource constraints. Reinforcement learning (RL) has been shown to be effective for IPP, however, it requires environment interactions, which are risky and expensive in practice. To address this problem, we propose an offline RL-based IPP framework that optimizes information gain without requiring real-time interaction during training, offering safety and cost-efficiency by avoiding interaction, as well as superior performance and fast computation during execution -- key advantages of RL. Our framework leverages batch-constrained reinforcement learning to mitigate extrapolation errors, enabling the agent to learn from pre-collected datasets generated by arbitrary algorithms. We validate the framework through extensive simulations and real-world experiments. The numerical results show that our framework outperforms the baselines, demonstrating the effectiveness of the proposed approach.

Spatio-temporal Motion Planning for Autonomous Vehicles with Trapezoidal Prism Corridors and Bézier Curves

Safety-guaranteed motion planning is critical for self-driving cars to generate collision-free trajectories. A layered motion planning approach with decoupled path and speed planning is widely used for this purpose. This approach is prone to be suboptimal in the presence of dynamic obstacles. Spatial-temporal approaches deal with path planning and speed planning simultaneously; however, the existing methods only support simple-shaped corridors like cuboids, which restrict the search space for optimization in complex scenarios. We propose to use trapezoidal prism-shaped corridors for optimization, which significantly enlarges the solution space compared to the existing cuboidal corridors-based method. Finally, a piecewise B\'{e}zier curve optimization is conducted in our proposed corridors. This formulation theoretically guarantees the safety of the continuous-time trajectory. We validate the efficiency and effectiveness of the proposed approach in numerical and CommonRoad simulations.