MonoCap: Monocular Human Motion Capture using a CNN Coupled with a Geometric Prior

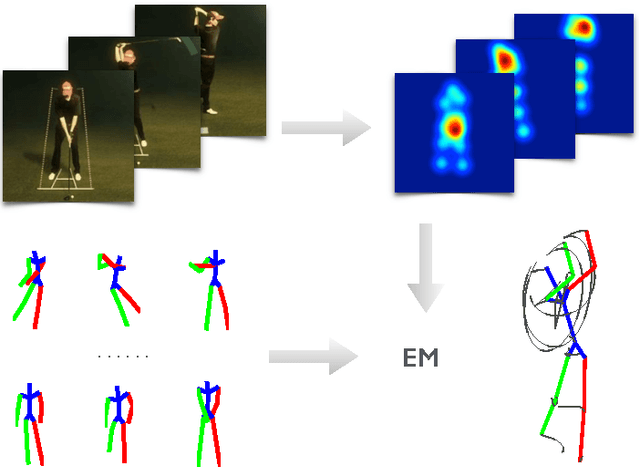
Recovering 3D full-body human pose is a challenging problem with many applications. It has been successfully addressed by motion capture systems with body worn markers and multiple cameras. In this paper, we address the more challenging case of not only using a single camera but also not leveraging markers: going directly from 2D appearance to 3D geometry. Deep learning approaches have shown remarkable abilities to discriminatively learn 2D appearance features. The missing piece is how to integrate 2D, 3D and temporal information to recover 3D geometry and account for the uncertainties arising from the discriminative model. We introduce a novel approach that treats 2D joint locations as latent variables whose uncertainty distributions are given by a deep fully convolutional neural network. The unknown 3D poses are modeled by a sparse representation and the 3D parameter estimates are realized via an Expectation-Maximization algorithm, where it is shown that the 2D joint location uncertainties can be conveniently marginalized out during inference. Extensive evaluation on benchmark datasets shows that the proposed approach achieves greater accuracy over state-of-the-art baselines. Notably, the proposed approach does not require synchronized 2D-3D data for training and is applicable to "in-the-wild" images, which is demonstrated with the MPII dataset.

Sparse Representation for 3D Shape Estimation: A Convex Relaxation Approach

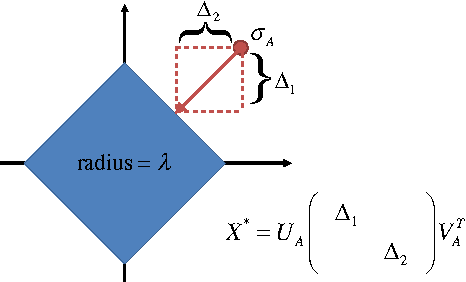
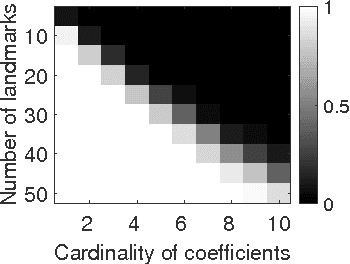
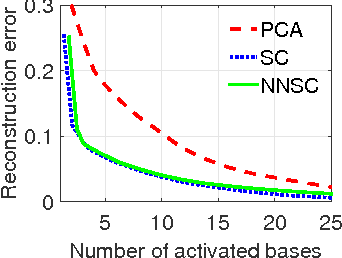
We investigate the problem of estimating the 3D shape of an object defined by a set of 3D landmarks, given their 2D correspondences in a single image. A successful approach to alleviating the reconstruction ambiguity is the 3D deformable shape model and a sparse representation is often used to capture complex shape variability. But the model inference is still a challenge due to the nonconvexity in optimization resulted from joint estimation of shape and viewpoint. In contrast to prior work that relies on a alternating scheme with solutions depending on initialization, we propose a convex approach to addressing this challenge and develop an efficient algorithm to solve the proposed convex program. Moreover, we propose a robust model to handle gross errors in the 2D correspondences. We demonstrate the exact recovery property of the proposed method, the advantage compared to the nonconvex baseline methods and the applicability to recover 3D human poses and car models from single images.

Distributed Consistent Data Association

Data association is one of the fundamental problems in multi-sensor systems. Most current techniques rely on pairwise data associations which can be spurious even after the employment of outlier rejection schemes. Considering multiple pairwise associations at once significantly increases accuracy and leads to consistency. In this work, we propose two fully decentralized methods for consistent global data association from pairwise data associations. The first method is a consensus algorithm on the set of doubly stochastic matrices. The second method is a decentralization of the spectral method proposed by Pachauri et al.. We demonstrate the effectiveness of both methods using theoretical analysis and experimental evaluation.

A Game-Theoretic Approach to Robust Fusion and Kalman Filtering Under Unknown Correlations

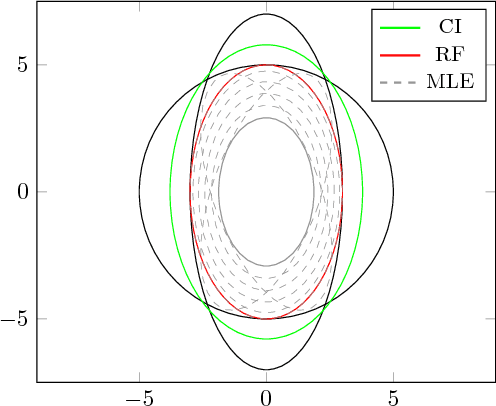
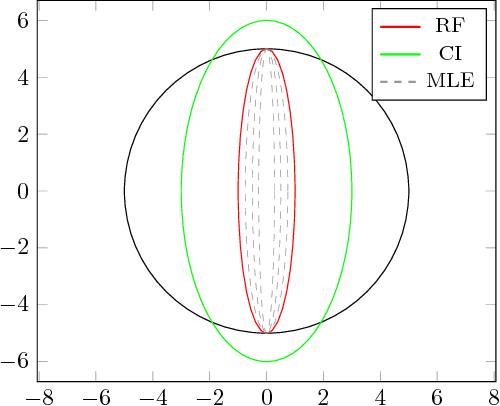
This work addresses the problem of fusing two random vectors with unknown cross-correlations. We present a formulation and a numerical method for computing the optimal estimate in the minimax sense. We extend our formulation to linear measurement models that depend on two random vectors with unknown cross-correlations. As an application we consider the problem of decentralized state estimation for a group of agents. The proposed estimator takes cross-correlations into account while being less conservative than the widely used Covariance Intersection. We demonstrate the superiority of the proposed method compared to Covariance Intersection with numerical examples and simulations within the specific application of decentralized state estimation using relative position measurements.

Sparseness Meets Deepness: 3D Human Pose Estimation from Monocular Video

This paper addresses the challenge of 3D full-body human pose estimation from a monocular image sequence. Here, two cases are considered: (i) the image locations of the human joints are provided and (ii) the image locations of joints are unknown. In the former case, a novel approach is introduced that integrates a sparsity-driven 3D geometric prior and temporal smoothness. In the latter case, the former case is extended by treating the image locations of the joints as latent variables. A deep fully convolutional network is trained to predict the uncertainty maps of the 2D joint locations. The 3D pose estimates are realized via an Expectation-Maximization algorithm over the entire sequence, where it is shown that the 2D joint location uncertainties can be conveniently marginalized out during inference. Empirical evaluation on the Human3.6M dataset shows that the proposed approaches achieve greater 3D pose estimation accuracy over state-of-the-art baselines. Further, the proposed approach outperforms a publicly available 2D pose estimation baseline on the challenging PennAction dataset.

3D Shape Estimation from 2D Landmarks: A Convex Relaxation Approach

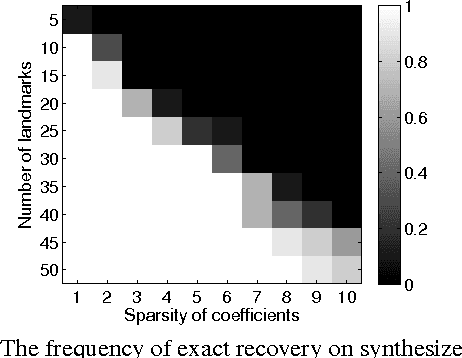
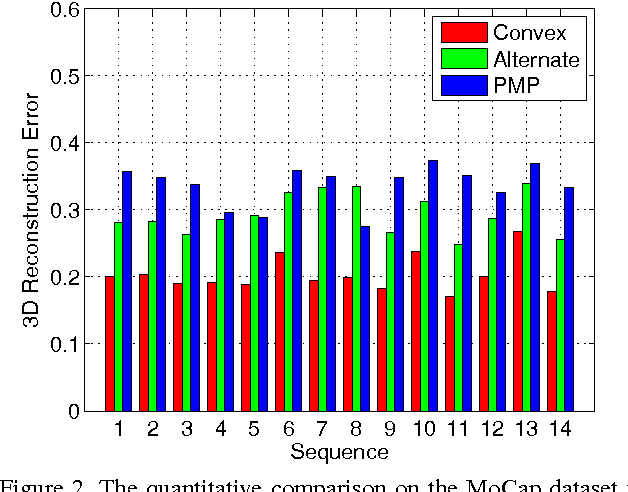
We investigate the problem of estimating the 3D shape of an object, given a set of 2D landmarks in a single image. To alleviate the reconstruction ambiguity, a widely-used approach is to confine the unknown 3D shape within a shape space built upon existing shapes. While this approach has proven to be successful in various applications, a challenging issue remains, i.e., the joint estimation of shape parameters and camera-pose parameters requires to solve a nonconvex optimization problem. The existing methods often adopt an alternating minimization scheme to locally update the parameters, and consequently the solution is sensitive to initialization. In this paper, we propose a convex formulation to address this problem and develop an efficient algorithm to solve the proposed convex program. We demonstrate the exact recovery property of the proposed method, its merits compared to alternative methods, and the applicability in human pose and car shape estimation.