A Game-Theoretic Approach to Robust Fusion and Kalman Filtering Under Unknown Correlations
Paper and Code
Oct 04, 2016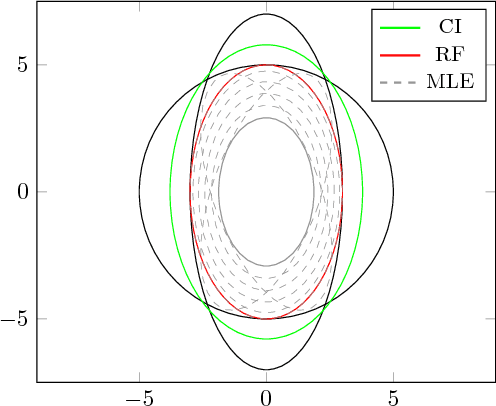
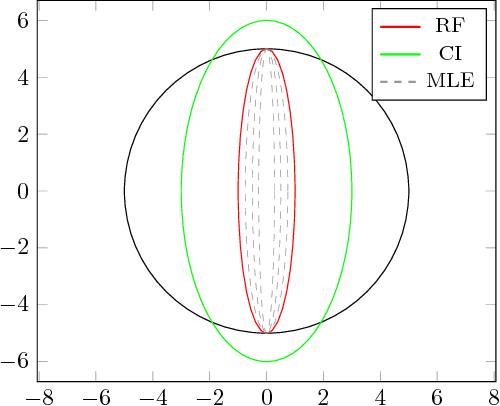


This work addresses the problem of fusing two random vectors with unknown cross-correlations. We present a formulation and a numerical method for computing the optimal estimate in the minimax sense. We extend our formulation to linear measurement models that depend on two random vectors with unknown cross-correlations. As an application we consider the problem of decentralized state estimation for a group of agents. The proposed estimator takes cross-correlations into account while being less conservative than the widely used Covariance Intersection. We demonstrate the superiority of the proposed method compared to Covariance Intersection with numerical examples and simulations within the specific application of decentralized state estimation using relative position measurements.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge