Semantic Graph Parsing with Recurrent Neural Network DAG Grammars

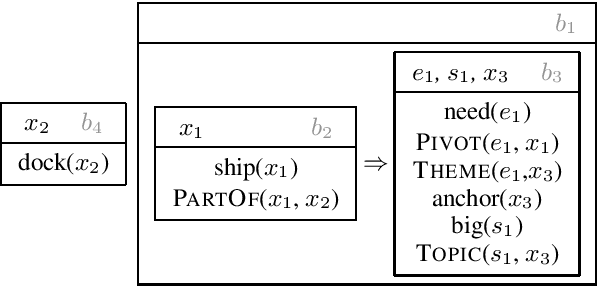
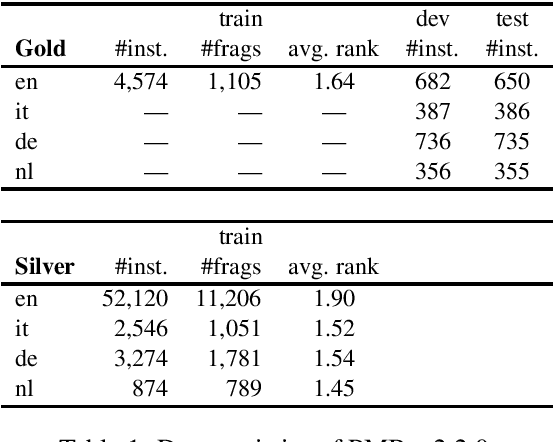
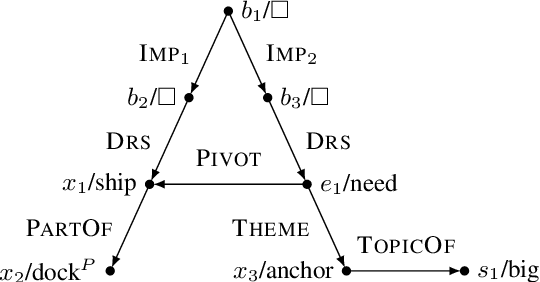
Semantic parses are directed acyclic graphs (DAGs), so semantic parsing should be modeled as graph prediction. But predicting graphs presents difficult technical challenges, so it is simpler and more common to predict the linearized graphs found in semantic parsing datasets using well-understood sequence models. The cost of this simplicity is that the predicted strings may not be well-formed graphs. We present recurrent neural network DAG grammars, a graph-aware sequence model that ensures only well-formed graphs while sidestepping many difficulties in graph prediction. We test our model on the Parallel Meaning Bank---a multilingual semantic graphbank. Our approach yields competitive results in English and establishes the first results for German, Italian and Dutch.

The problem with probabilistic DAG automata for semantic graphs

Semantic representations in the form of directed acyclic graphs (DAGs) have been introduced in recent years, and to model them, we need probabilistic models of DAGs. One model that has attracted some attention is the DAG automaton, but it has not been studied as a probabilistic model. We show that some DAG automata cannot be made into useful probabilistic models by the nearly universal strategy of assigning weights to transitions. The problem affects single-rooted, multi-rooted, and unbounded-degree variants of DAG automata, and appears to be pervasive. It does not affect planar variants, but these are problematic for other reasons.

Recurrent Neural Networks as Weighted Language Recognizers

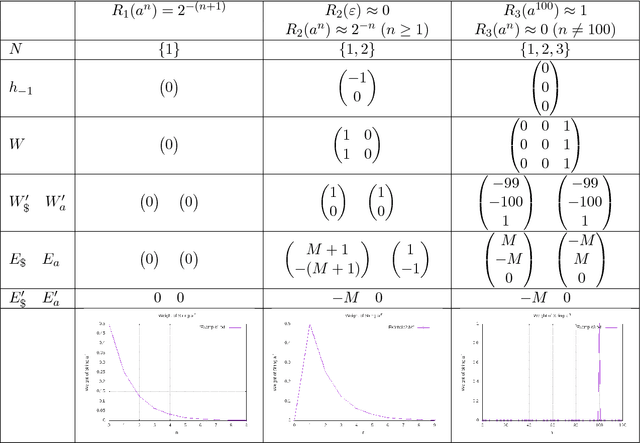
We investigate the computational complexity of various problems for simple recurrent neural networks (RNNs) as formal models for recognizing weighted languages. We focus on the single-layer, ReLU-activation, rational-weight RNNs with softmax, which are commonly used in natural language processing applications. We show that most problems for such RNNs are undecidable, including consistency, equivalence, minimization, and the determination of the highest-weighted string. However, for consistent RNNs the last problem becomes decidable, although the solution length can surpass all computable bounds. If additionally the string is limited to polynomial length, the problem becomes NP-complete and APX-hard. In summary, this shows that approximations and heuristic algorithms are necessary in practical applications of those RNNs.