Strong Equivalence of TAG and CCG

Tree-adjoining grammar (TAG) and combinatory categorial grammar (CCG) are two well-established mildly context-sensitive grammar formalisms that are known to have the same expressive power on strings (i.e., generate the same class of string languages). It is demonstrated that their expressive power on trees also essentially coincides. In fact, CCG without lexicon entries for the empty string and only first-order rules of degree at most 2 are sufficient for its full expressive power.

Recurrent Neural Networks as Weighted Language Recognizers

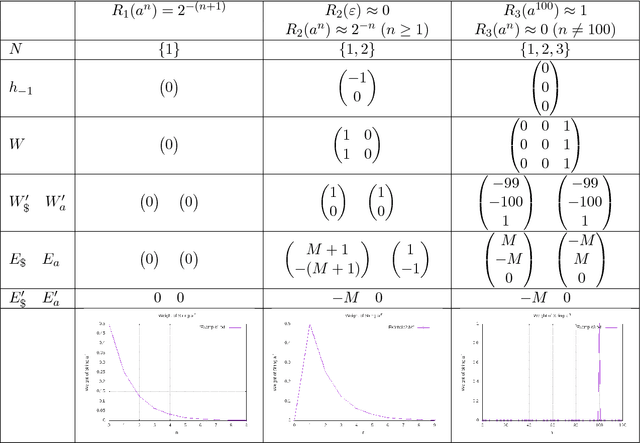
We investigate the computational complexity of various problems for simple recurrent neural networks (RNNs) as formal models for recognizing weighted languages. We focus on the single-layer, ReLU-activation, rational-weight RNNs with softmax, which are commonly used in natural language processing applications. We show that most problems for such RNNs are undecidable, including consistency, equivalence, minimization, and the determination of the highest-weighted string. However, for consistent RNNs the last problem becomes decidable, although the solution length can surpass all computable bounds. If additionally the string is limited to polynomial length, the problem becomes NP-complete and APX-hard. In summary, this shows that approximations and heuristic algorithms are necessary in practical applications of those RNNs.

Multiple Context-Free Tree Grammars: Lexicalization and Characterization

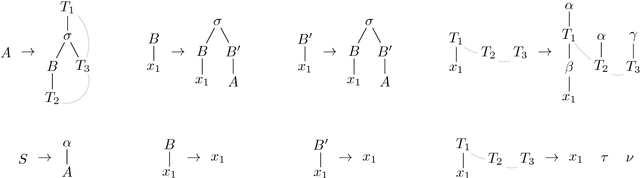
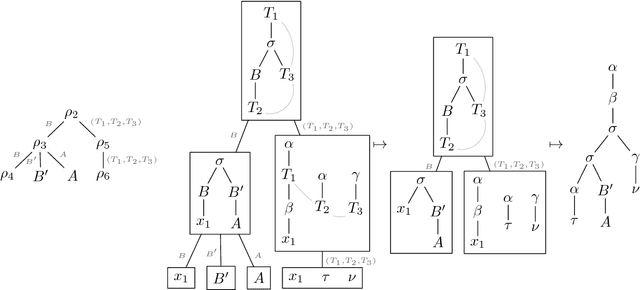
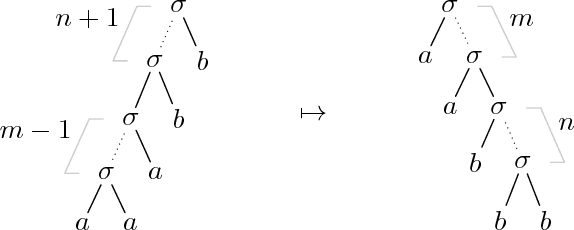
Multiple (simple) context-free tree grammars are investigated, where "simple" means "linear and nondeleting". Every multiple context-free tree grammar that is finitely ambiguous can be lexicalized; i.e., it can be transformed into an equivalent one (generating the same tree language) in which each rule of the grammar contains a lexical symbol. Due to this transformation, the rank of the nonterminals increases at most by 1, and the multiplicity (or fan-out) of the grammar increases at most by the maximal rank of the lexical symbols; in particular, the multiplicity does not increase when all lexical symbols have rank 0. Multiple context-free tree grammars have the same tree generating power as multi-component tree adjoining grammars (provided the latter can use a root-marker). Moreover, every multi-component tree adjoining grammar that is finitely ambiguous can be lexicalized. Multiple context-free tree grammars have the same string generating power as multiple context-free (string) grammars and polynomial time parsing algorithms. A tree language can be generated by a multiple context-free tree grammar if and only if it is the image of a regular tree language under a deterministic finite-copying macro tree transducer. Multiple context-free tree grammars can be used as a synchronous translation device.

Properties of quasi-alphabetic tree bimorphisms

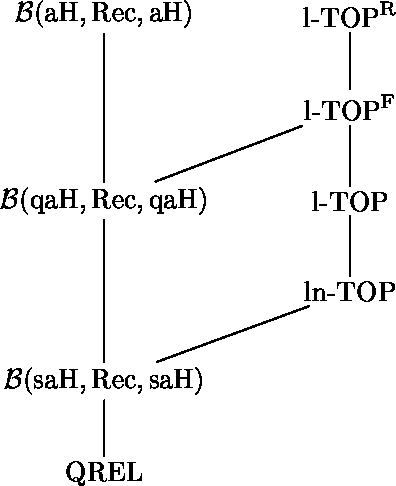
We study the class of quasi-alphabetic relations, i.e., tree transformations defined by tree bimorphisms with two quasi-alphabetic tree homomorphisms and a regular tree language. We present a canonical representation of these relations; as an immediate consequence, we get the closure under union. Also, we show that they are not closed under intersection and complement, and do not preserve most common operations on trees (branches, subtrees, v-product, v-quotient, f-top-catenation). Moreover, we prove that the translations defined by quasi-alphabetic tree bimorphism are exactly products of context-free string languages. We conclude by presenting the connections between quasi-alphabetic relations, alphabetic relations and classes of tree transformations defined by several types of top-down tree transducers. Furthermore, we get that quasi-alphabetic relations preserve the recognizable and algebraic tree languages.