Properties of quasi-alphabetic tree bimorphisms
Paper and Code
Jun 12, 2009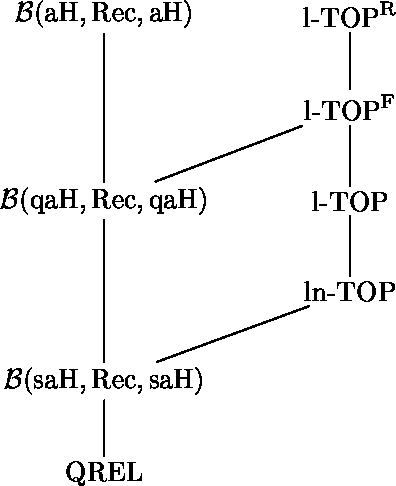
We study the class of quasi-alphabetic relations, i.e., tree transformations defined by tree bimorphisms with two quasi-alphabetic tree homomorphisms and a regular tree language. We present a canonical representation of these relations; as an immediate consequence, we get the closure under union. Also, we show that they are not closed under intersection and complement, and do not preserve most common operations on trees (branches, subtrees, v-product, v-quotient, f-top-catenation). Moreover, we prove that the translations defined by quasi-alphabetic tree bimorphism are exactly products of context-free string languages. We conclude by presenting the connections between quasi-alphabetic relations, alphabetic relations and classes of tree transformations defined by several types of top-down tree transducers. Furthermore, we get that quasi-alphabetic relations preserve the recognizable and algebraic tree languages.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge