s2n-bignum-bench: A practical benchmark for evaluating low-level code reasoning of LLMs

Neurosymbolic approaches leveraging Large Language Models (LLMs) with formal methods have recently achieved strong results on mathematics-oriented theorem-proving benchmarks. However, success on competition-style mathematics does not by itself demonstrate the ability to construct proofs about real-world implementations. We address this gap with a benchmark derived from an industrial cryptographic library whose assembly routines are already verified in HOL Light. s2n-bignum is a library used at AWS for providing fast assembly routines for cryptography, and its correctness is established by formal verification. The task of formally verifying this library has been a significant achievement for the Automated Reasoning Group. It involved two tasks: (1) precisely specifying the correct behavior of a program as a mathematical proposition, and (2) proving that the proposition is correct. In the case of s2n-bignum, both tasks were carried out by human experts. In \textit{s2n-bignum-bench}, we provide the formal specification and ask the LLM to generate a proof script that is accepted by HOL Light within a fixed proof-check timeout. To our knowledge, \textit{s2n-bignum-bench} is the first public benchmark focused on machine-checkable proof synthesis for industrial low-level cryptographic assembly routines in HOL Light. This benchmark provides a challenging and practically relevant testbed for evaluating LLM-based theorem proving beyond competition mathematics. The code to set up and use the benchmark is available here: \href{https://github.com/kings-crown/s2n-bignum-bench}{s2n-bignum-bench}.

Learning Adaptive LLM Decoding

Decoding from large language models (LLMs) typically relies on fixed sampling hyperparameters (e.g., temperature, top-p), despite substantial variation in task difficulty and uncertainty across prompts and individual decoding steps. We propose to learn adaptive decoding policies that dynamically select sampling strategies at inference time, conditioned on available compute resources. Rather than fine-tuning the language model itself, we introduce lightweight decoding adapters trained with reinforcement learning and verifiable terminal rewards (e.g. correctness on math and coding tasks). At the sequence level, we frame decoding as a contextual bandit problem: a policy selects a decoding strategy (e.g. greedy, top-k, min-p) for each prompt, conditioned on the prompt embedding and a parallel sampling budget. At the token level, we model decoding as a partially observable Markov decision process (POMDP), where a policy selects sampling actions at each token step based on internal model features and the remaining token budget. Experiments on the MATH and CodeContests benchmarks show that the learned adapters improve the accuracy-budget tradeoff: on MATH, the token-level adapter improves Pass@1 accuracy by up to 10.2% over the best static baseline under a fixed token budget, while the sequence-level adapter yields 2-3% gains under fixed parallel sampling. Ablation analyses support the contribution of both sequence- and token-level adaptation.

Certified Control: An Architecture for Verifiable Safety of Autonomous Vehicles

Widespread adoption of autonomous cars will require greater confidence in their safety than is currently possible. Certified control is a new safety architecture whose goal is two-fold: to achieve a very high level of safety, and to provide a framework for justifiable confidence in that safety. The key idea is a runtime monitor that acts, along with sensor hardware and low-level control and actuators, as a small trusted base, ensuring the safety of the system as a whole. Unfortunately, in current systems complex perception makes the verification even of a runtime monitor challenging. Unlike traditional runtime monitoring, therefore, a certified control monitor does not perform perception and analysis itself. Instead, the main controller assembles evidence that the proposed action is safe into a certificate that is then checked independently by the monitor. This exploits the classic gap between the costs of finding and checking. The controller is assigned the task of finding the certificate, and can thus use the most sophisticated algorithms available (including learning-enabled software); the monitor is assigned only the task of checking, and can thus run quickly and be smaller and formally verifiable. This paper explains the key ideas of certified control and illustrates them with a certificate for LiDAR data and its formal verification. It shows how the architecture dramatically reduces the amount of code to be verified, providing an end-to-end safety analysis that would likely not be achievable in a traditional architecture.

Better AI through Logical Scaffolding

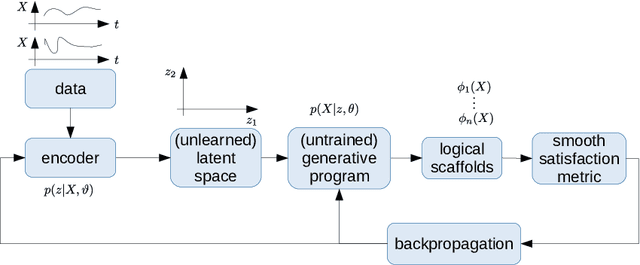
We describe the concept of logical scaffolds, which can be used to improve the quality of software that relies on AI components. We explain how some of the existing ideas on runtime monitors for perception systems can be seen as a specific instance of logical scaffolds. Furthermore, we describe how logical scaffolds may be useful for improving AI programs beyond perception systems, to include general prediction systems and agent behavior models.

REAS: Combining Numerical Optimization with SAT Solving

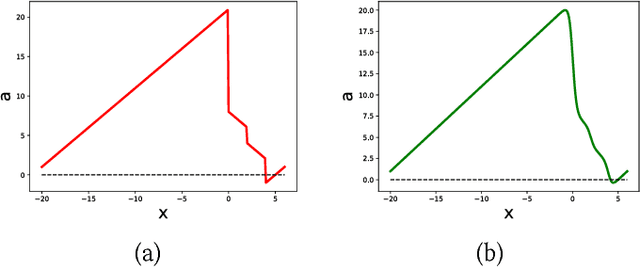
In this paper, we present ReaS, a technique that combines numerical optimization with SAT solving to synthesize unknowns in a program that involves discrete and floating point computation. ReaS makes the program end-to-end differentiable by smoothing any Boolean expression that introduces discontinuity such as conditionals and relaxing the Boolean unknowns so that numerical optimization can be performed. On top of this, ReaS uses a SAT solver to help the numerical search overcome local solutions by incrementally fixing values to the Boolean expressions. We evaluated the approach on 5 case studies involving hybrid systems and show that ReaS can synthesize programs that could not be solved by previous SMT approaches.