PETformer: Long-term Time Series Forecasting via Placeholder-enhanced Transformer

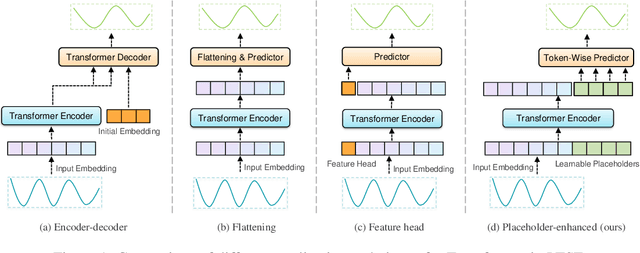
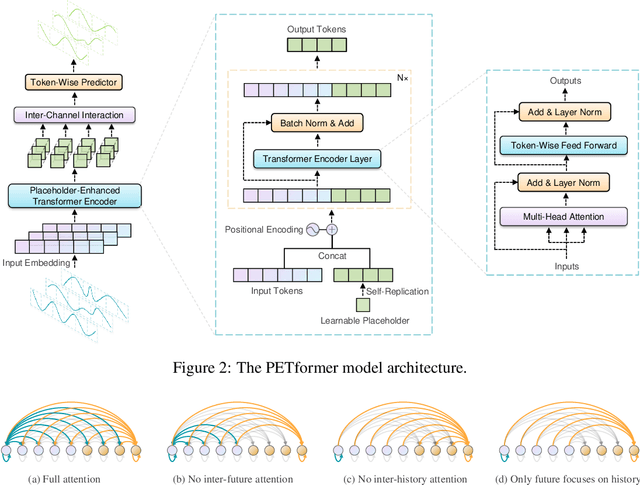
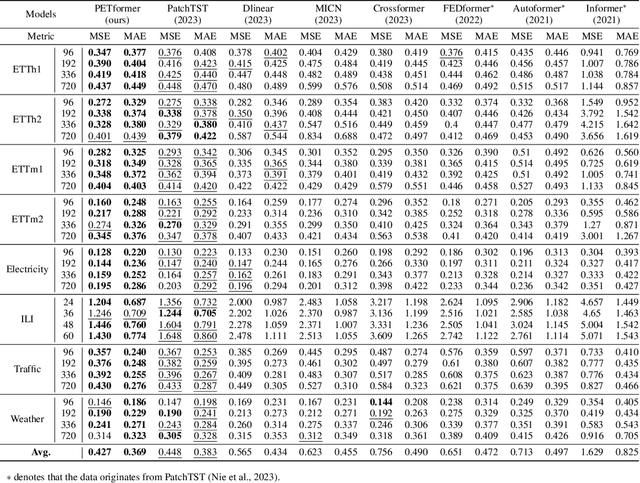
Recently, Transformer-based models have shown remarkable performance in long-term time series forecasting (LTSF) tasks due to their ability to model long-term dependencies. However, the validity of Transformers for LTSF tasks remains debatable, particularly since recent work has shown that simple linear models can outperform numerous Transformer-based approaches. This suggests that there are limitations to the application of Transformer in LTSF. Therefore, this paper investigates three key issues when applying Transformer to LTSF: temporal continuity, information density, and multi-channel relationships. Accordingly, we propose three innovative solutions, including Placeholder Enhancement Technique (PET), Long Sub-sequence Division (LSD), and Multi-channel Separation and Interaction (MSI), which together form a novel model called PETformer. These three key designs introduce prior biases suitable for LTSF tasks. Extensive experiments have demonstrated that PETformer achieves state-of-the-art (SOTA) performance on eight commonly used public datasets for LTSF, outperforming all other models currently available. This demonstrates that Transformer still possesses powerful capabilities in LTSF.

Mean Field Optimization Problem Regularized by Fisher Information

Recently there is a rising interest in the research of mean field optimization, in particular because of its role in analyzing the training of neural networks. In this paper by adding the Fisher Information as the regularizer, we relate the regularized mean field optimization problem to a so-called mean field Schrodinger dynamics. We develop an energy-dissipation method to show that the marginal distributions of the mean field Schrodinger dynamics converge exponentially quickly towards the unique minimizer of the regularized optimization problem. Remarkably, the mean field Schrodinger dynamics is proved to be a gradient flow on the probability measure space with respect to the relative entropy. Finally we propose a Monte Carlo method to sample the marginal distributions of the mean field Schrodinger dynamics.

Uniform-in-Time Propagation of Chaos for Mean Field Langevin Dynamics

We study the uniform-in-time propagation of chaos for mean field Langevin dynamics with convex mean field potenital. Convergences in both Wasserstein-$2$ distance and relative entropy are established. We do not require the mean field potenital functional to bear either small mean field interaction or displacement convexity, which are common constraints in the literature. In particular, it allows us to study the efficiency of the noisy gradient descent algorithm for training two-layer neural networks.