Mean Field Optimization Problem Regularized by Fisher Information

Recently there is a rising interest in the research of mean field optimization, in particular because of its role in analyzing the training of neural networks. In this paper by adding the Fisher Information as the regularizer, we relate the regularized mean field optimization problem to a so-called mean field Schrodinger dynamics. We develop an energy-dissipation method to show that the marginal distributions of the mean field Schrodinger dynamics converge exponentially quickly towards the unique minimizer of the regularized optimization problem. Remarkably, the mean field Schrodinger dynamics is proved to be a gradient flow on the probability measure space with respect to the relative entropy. Finally we propose a Monte Carlo method to sample the marginal distributions of the mean field Schrodinger dynamics.

Uniform-in-Time Propagation of Chaos for Mean Field Langevin Dynamics

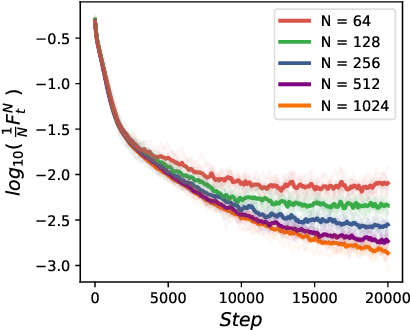
We study the uniform-in-time propagation of chaos for mean field Langevin dynamics with convex mean field potenital. Convergences in both Wasserstein-$2$ distance and relative entropy are established. We do not require the mean field potenital functional to bear either small mean field interaction or displacement convexity, which are common constraints in the literature. In particular, it allows us to study the efficiency of the noisy gradient descent algorithm for training two-layer neural networks.

Ergodicity of the underdamped mean-field Langevin dynamics

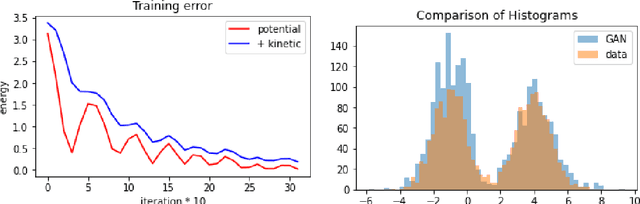
We study the long time behavior of an underdamped mean-field Langevin (MFL) equation, and provide a general convergence as well as an exponential convergence rate result under different conditions. The results on the MFL equation can be applied to study the convergence of the Hamiltonian gradient descent algorithm for the overparametrized optimization. We then provide a numerical example of the algorithm to train a generative adversarial networks (GAN).

Game on Random Environment, Mean-field Langevin System and Neural Networks

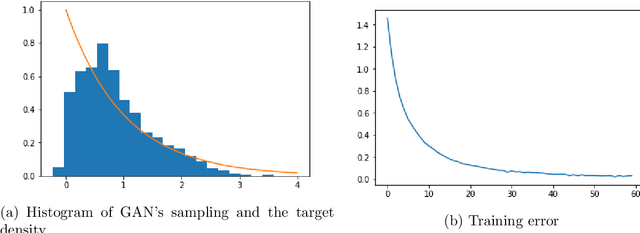
In this paper we study a type of games regularized by the relative entropy, where the players' strategies are coupled through a random environment variable. Besides the existence and the uniqueness of equilibria of such games, we prove that the marginal laws of the corresponding mean-field Langevin systems can converge towards the games' equilibria in different settings. As applications, the dynamic games can be treated as games on a random environment when one treats the time horizon as the environment. In practice, our results can be applied to analysing the stochastic gradient descent algorithm for deep neural networks in the context of supervised learning as well as for the generative adversarial networks.

Mean-field Langevin System, Optimal Control and Deep Neural Networks

In this paper, we study a regularised relaxed optimal control problem and, in particular, we are concerned with the case where the control variable is of large dimension. We introduce a system of mean-field Langevin equations, the invariant measure of which is shown to be the optimal control of the initial problem under mild conditions. Therefore, this system of processes can be viewed as a continuous-time numerical algorithm for computing the optimal control. As an application, this result endorses the solvability of the stochastic gradient descent algorithm for a wide class of deep neural networks.

Mean-Field Langevin Dynamics and Energy Landscape of Neural Networks

We present a probabilistic analysis of the long-time behaviour of the nonlocal, diffusive equations with a gradient flow structure in 2-Wasserstein metric, namely, the Mean-Field Langevin Dynamics (MFLD). Our work is motivated by a desire to provide a theoretical underpinning for the convergence of stochastic gradient type algorithms widely used for non-convex learning tasks such as training of deep neural networks. The key insight is that the certain class of the finite dimensional non-convex problems becomes convex when lifted to infinite dimensional space of measures. We leverage this observation and show that the corresponding energy functional defined on the space of probability measures has a unique minimiser which can be characterised by a first order condition using the notion of linear functional derivative. Next, we show that the flow of marginal laws induced by the MFLD converges to the stationary distribution which is exactly the minimiser of the energy functional. We show that this convergence is exponential under conditions that are satisfied for highly regularised learning tasks. At the heart of our analysis is a pathwise perspective on Otto calculus used in gradient flow literature which is of independent interest. Our proof of convergence to stationary probability measure is novel and it relies on a generalisation of LaSalle's invariance principle. Importantly we do not assume that interaction potential of MFLD is of convolution type nor that has any particular symmetric structure. This is critical for applications. Finally, we show that the error between finite dimensional optimisation problem and its infinite dimensional limit is of order one over the number of parameters.