Ergodicity of the underdamped mean-field Langevin dynamics

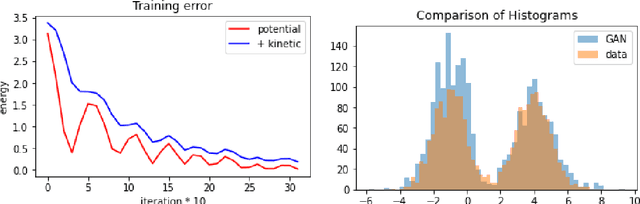
We study the long time behavior of an underdamped mean-field Langevin (MFL) equation, and provide a general convergence as well as an exponential convergence rate result under different conditions. The results on the MFL equation can be applied to study the convergence of the Hamiltonian gradient descent algorithm for the overparametrized optimization. We then provide a numerical example of the algorithm to train a generative adversarial networks (GAN).

Game on Random Environment, Mean-field Langevin System and Neural Networks

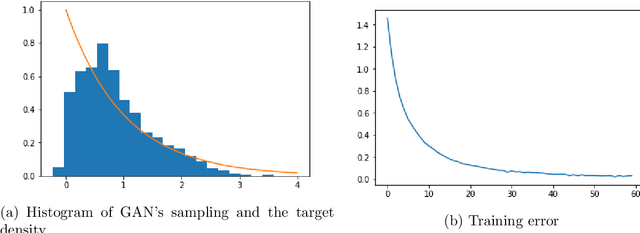
In this paper we study a type of games regularized by the relative entropy, where the players' strategies are coupled through a random environment variable. Besides the existence and the uniqueness of equilibria of such games, we prove that the marginal laws of the corresponding mean-field Langevin systems can converge towards the games' equilibria in different settings. As applications, the dynamic games can be treated as games on a random environment when one treats the time horizon as the environment. In practice, our results can be applied to analysing the stochastic gradient descent algorithm for deep neural networks in the context of supervised learning as well as for the generative adversarial networks.

Mean-field Langevin System, Optimal Control and Deep Neural Networks

In this paper, we study a regularised relaxed optimal control problem and, in particular, we are concerned with the case where the control variable is of large dimension. We introduce a system of mean-field Langevin equations, the invariant measure of which is shown to be the optimal control of the initial problem under mild conditions. Therefore, this system of processes can be viewed as a continuous-time numerical algorithm for computing the optimal control. As an application, this result endorses the solvability of the stochastic gradient descent algorithm for a wide class of deep neural networks.