Uncertainty Quantification in Inverse Models in Hydrology

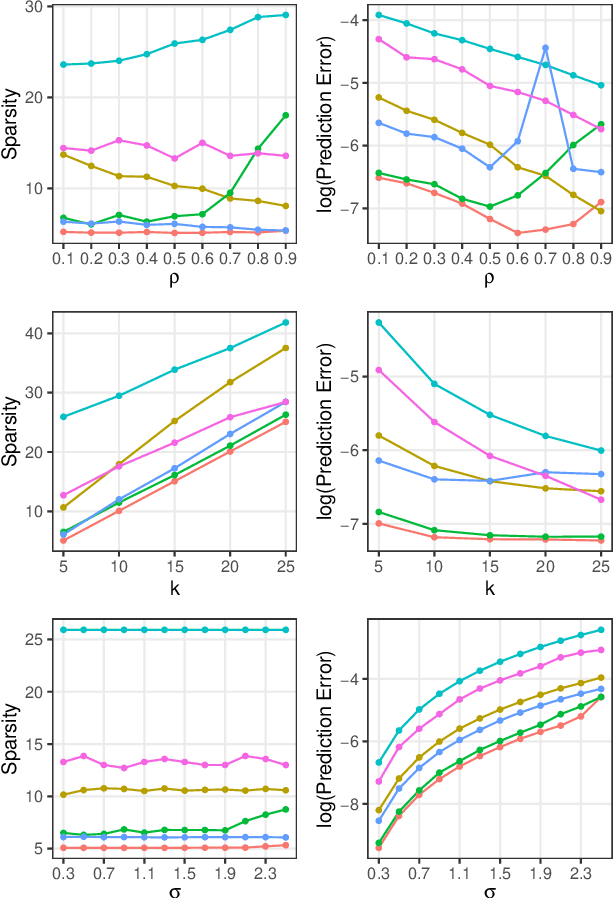
In hydrology, modeling streamflow remains a challenging task due to the limited availability of basin characteristics information such as soil geology and geomorphology. These characteristics may be noisy due to measurement errors or may be missing altogether. To overcome this challenge, we propose a knowledge-guided, probabilistic inverse modeling method for recovering physical characteristics from streamflow and weather data, which are more readily available. We compare our framework with state-of-the-art inverse models for estimating river basin characteristics. We also show that these estimates offer improvement in streamflow modeling as opposed to using the original basin characteristic values. Our inverse model offers 3\% improvement in R$^2$ for the inverse model (basin characteristic estimation) and 6\% for the forward model (streamflow prediction). Our framework also offers improved explainability since it can quantify uncertainty in both the inverse and the forward model. Uncertainty quantification plays a pivotal role in improving the explainability of machine learning models by providing additional insights into the reliability and limitations of model predictions. In our analysis, we assess the quality of the uncertainty estimates. Compared to baseline uncertainty quantification methods, our framework offers 10\% improvement in the dispersion of epistemic uncertainty and 13\% improvement in coverage rate. This information can help stakeholders understand the level of uncertainty associated with the predictions and provide a more comprehensive view of the potential outcomes.

Probabilistic Inverse Modeling: An Application in Hydrology

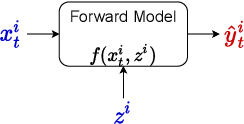
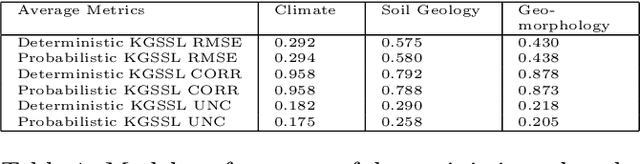
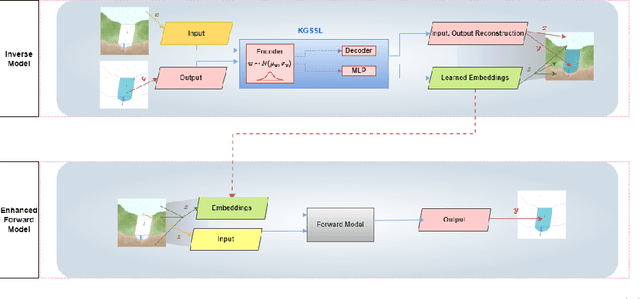
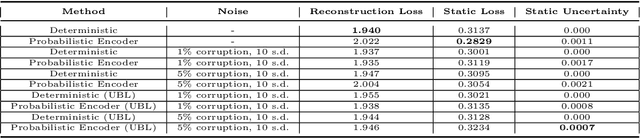
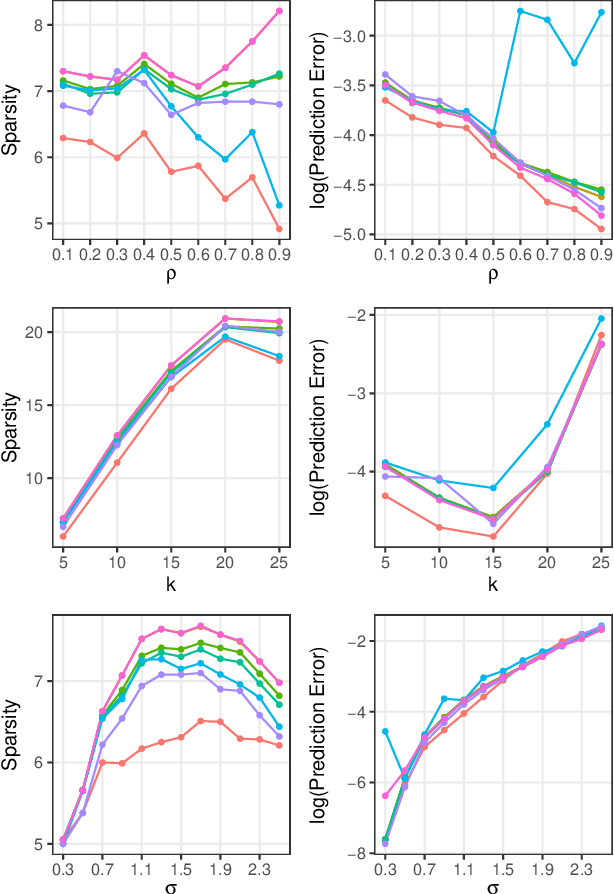
The astounding success of these methods has made it imperative to obtain more explainable and trustworthy estimates from these models. In hydrology, basin characteristics can be noisy or missing, impacting streamflow prediction. For solving inverse problems in such applications, ensuring explainability is pivotal for tackling issues relating to data bias and large search space. We propose a probabilistic inverse model framework that can reconstruct robust hydrology basin characteristics from dynamic input weather driver and streamflow response data. We address two aspects of building more explainable inverse models, uncertainty estimation and robustness. This can help improve the trust of water managers, handling of noisy data and reduce costs. We propose uncertainty based learning method that offers 6\% improvement in $R^2$ for streamflow prediction (forward modeling) from inverse model inferred basin characteristic estimates, 17\% reduction in uncertainty (40\% in presence of noise) and 4\% higher coverage rate for basin characteristics.

Feature Selection using e-values

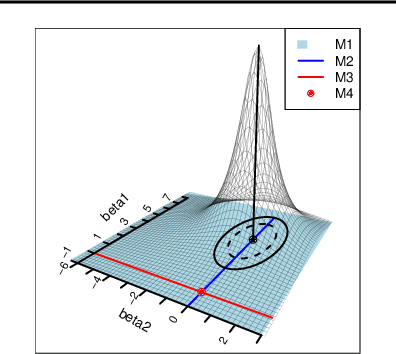
In the context of supervised parametric models, we introduce the concept of e-values. An e-value is a scalar quantity that represents the proximity of the sampling distribution of parameter estimates in a model trained on a subset of features to that of the model trained on all features (i.e. the full model). Under general conditions, a rank ordering of e-values separates models that contain all essential features from those that do not. The e-values are applicable to a wide range of parametric models. We use data depths and a fast resampling-based algorithm to implement a feature selection procedure using e-values, providing consistency results. For a $p$-dimensional feature space, this procedure requires fitting only the full model and evaluating $p+1$ models, as opposed to the traditional requirement of fitting and evaluating $2^p$ models. Through experiments across several model settings and synthetic and real datasets, we establish that the e-values method as a promising general alternative to existing model-specific methods of feature selection.

Approximate Bayesian Computation for Physical Inverse Modeling

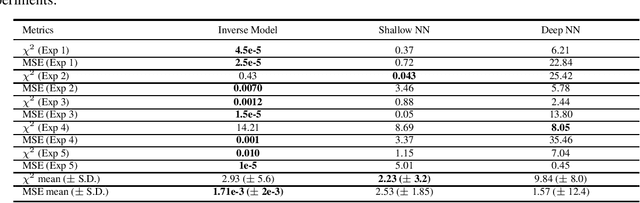
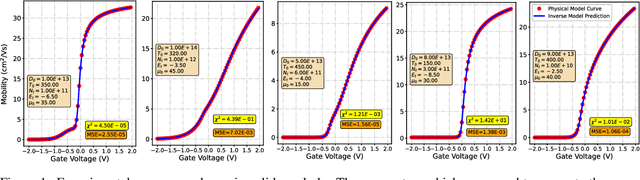
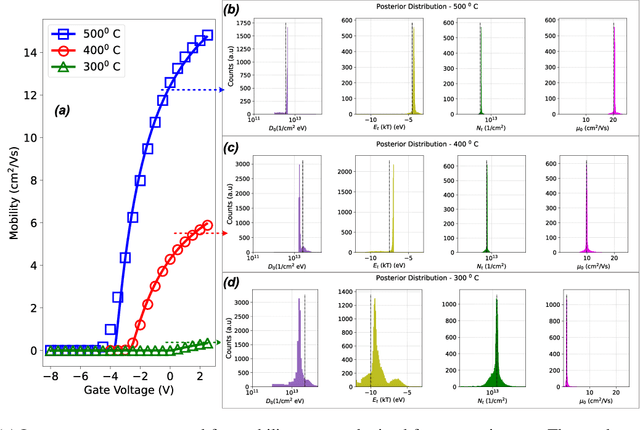
Semiconductor device models are essential to understand the charge transport in thin film transistors (TFTs). Using these TFT models to draw inference involves estimating parameters used to fit to the experimental data. These experimental data can involve extracted charge carrier mobility or measured current. Estimating these parameters help us draw inferences about device performance. Fitting a TFT model for a given experimental data using the model parameters relies on manual fine tuning of multiple parameters by human experts. Several of these parameters may have confounding effects on the experimental data, making their individual effect extraction a non-intuitive process during manual tuning. To avoid this convoluted process, we propose a new method for automating the model parameter extraction process resulting in an accurate model fitting. In this work, model choice based approximate Bayesian computation (aBc) is used for generating the posterior distribution of the estimated parameters using observed mobility at various gate voltage values. Furthermore, it is shown that the extracted parameters can be accurately predicted from the mobility curves using gradient boosted trees. This work also provides a comparative analysis of the proposed framework with fine-tuned neural networks wherein the proposed framework is shown to perform better.

Generalized Multivariate Signs for Nonparametric Hypothesis Testing in High Dimensions

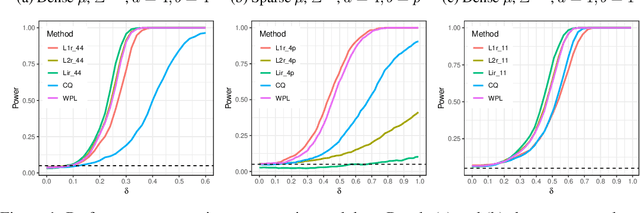
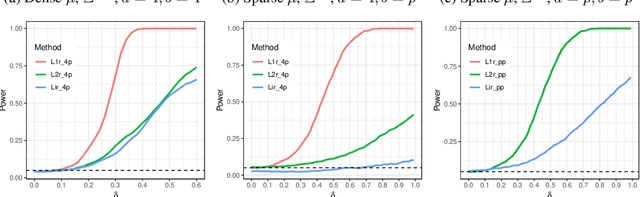
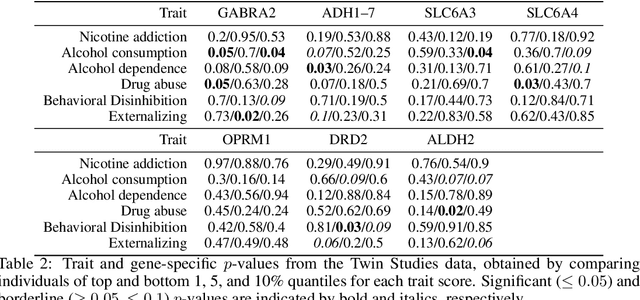
High-dimensional data, where the dimension of the feature space is much larger than sample size, arise in a number of statistical applications. In this context, we construct the generalized multivariate sign transformation, defined as a vector divided by its norm. For different choices of the norm function, the resulting transformed vector adapts to certain geometrical features of the data distribution. Building up on this idea, we obtain one-sample and two-sample testing procedures for mean vectors of high-dimensional data using these generalized sign vectors. These tests are based on U-statistics using kernel inner products, do not require prohibitive assumptions, and are amenable to a fast randomization-based implementation. Through experiments in a number of data settings, we show that tests using generalized signs display higher power than existing tests, while maintaining nominal type-I error rates. Finally, we provide example applications on the MNIST and Minnesota Twin Studies genomic data.

A Fast-Optimal Guaranteed Algorithm For Learning Sub-Interval Relationships in Time Series

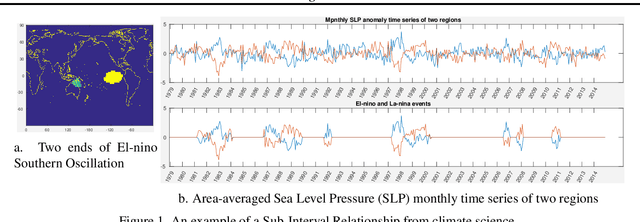
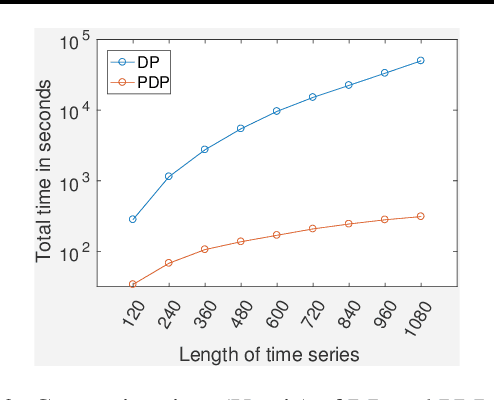
Traditional approaches focus on finding relationships between two entire time series, however, many interesting relationships exist in small sub-intervals of time and remain feeble during other sub-intervals. We define the notion of a sub-interval relationship (SIR) to capture such interactions that are prominent only in certain sub-intervals of time. To that end, we propose a fast-optimal guaranteed algorithm to find most interesting SIR relationship in a pair of time series. Lastly, we demonstrate the utility of our method in climate science domain based on a real-world dataset along with its scalability scope and obtain useful domain insights.

Mining Sub-Interval Relationships In Time Series Data

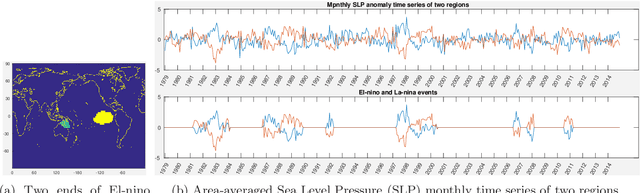
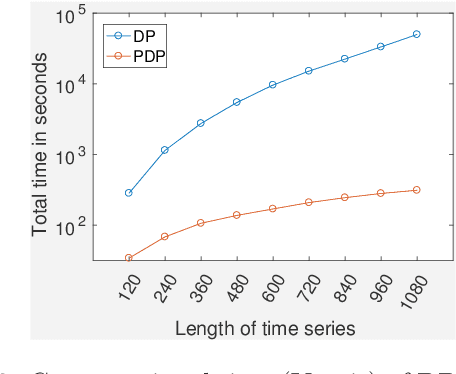
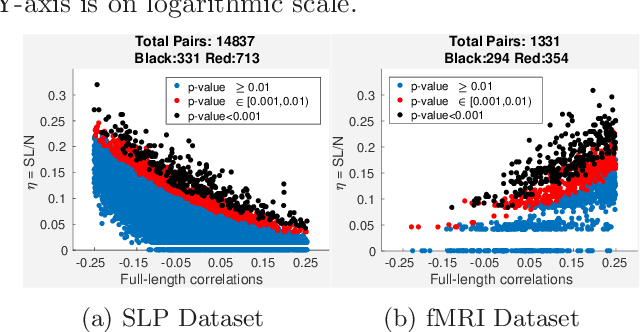
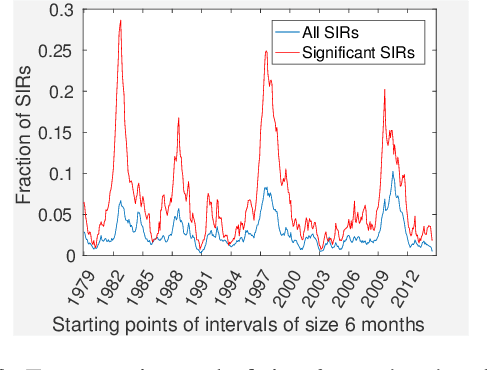
Time-series data is being increasingly collected and stud- ied in several areas such as neuroscience, climate science, transportation, and social media. Discovery of complex patterns of relationships between individual time-series, using data-driven approaches can improve our understanding of real-world systems. While traditional approaches typically study relationships between two entire time series, many interesting relationships in real-world applications exist in small sub-intervals of time while remaining absent or feeble during other sub-intervals. In this paper, we define the notion of a sub-interval relationship (SIR) to capture inter- actions between two time series that are prominent only in certain sub-intervals of time. We propose a novel and efficient approach to find most interesting SIR in a pair of time series. We evaluate our proposed approach on two real-world datasets from climate science and neuroscience domain and demonstrated the scalability and computational efficiency of our proposed approach. We further evaluated our discovered SIRs based on a randomization based procedure. Our results indicated the existence of several such relationships that are statistically significant, some of which were also found to have physical interpretation.