Generalized Multivariate Signs for Nonparametric Hypothesis Testing in High Dimensions
Paper and Code
Jul 02, 2021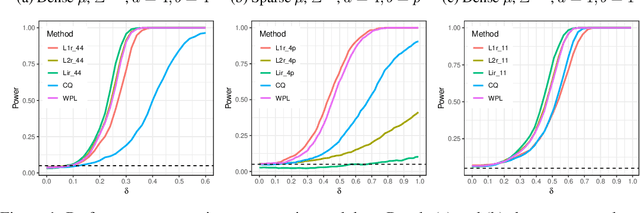

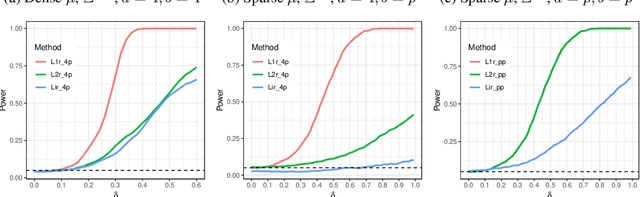
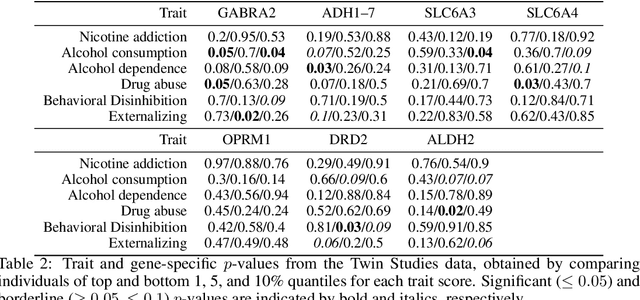
High-dimensional data, where the dimension of the feature space is much larger than sample size, arise in a number of statistical applications. In this context, we construct the generalized multivariate sign transformation, defined as a vector divided by its norm. For different choices of the norm function, the resulting transformed vector adapts to certain geometrical features of the data distribution. Building up on this idea, we obtain one-sample and two-sample testing procedures for mean vectors of high-dimensional data using these generalized sign vectors. These tests are based on U-statistics using kernel inner products, do not require prohibitive assumptions, and are amenable to a fast randomization-based implementation. Through experiments in a number of data settings, we show that tests using generalized signs display higher power than existing tests, while maintaining nominal type-I error rates. Finally, we provide example applications on the MNIST and Minnesota Twin Studies genomic data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge