Feature Selection using e-values
Paper and Code
Jun 16, 2022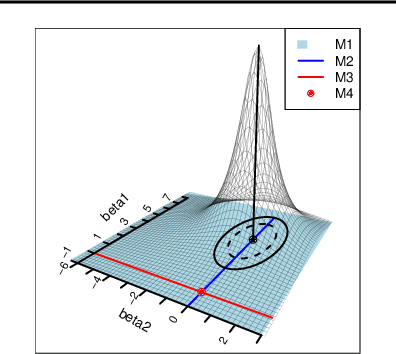
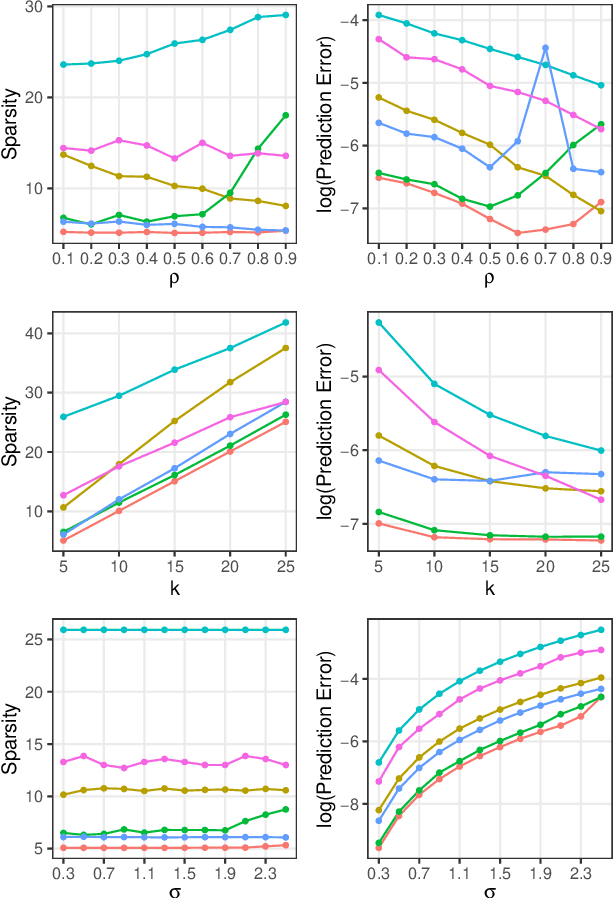

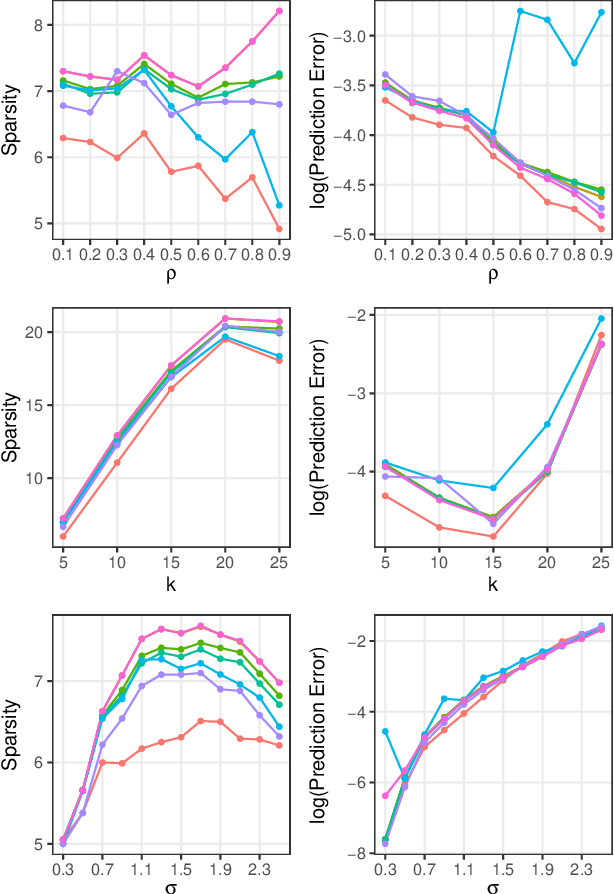
In the context of supervised parametric models, we introduce the concept of e-values. An e-value is a scalar quantity that represents the proximity of the sampling distribution of parameter estimates in a model trained on a subset of features to that of the model trained on all features (i.e. the full model). Under general conditions, a rank ordering of e-values separates models that contain all essential features from those that do not. The e-values are applicable to a wide range of parametric models. We use data depths and a fast resampling-based algorithm to implement a feature selection procedure using e-values, providing consistency results. For a $p$-dimensional feature space, this procedure requires fitting only the full model and evaluating $p+1$ models, as opposed to the traditional requirement of fitting and evaluating $2^p$ models. Through experiments across several model settings and synthetic and real datasets, we establish that the e-values method as a promising general alternative to existing model-specific methods of feature selection.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge