Gowtham Atluri
Mining Sub-Interval Relationships In Time Series Data
Feb 16, 2018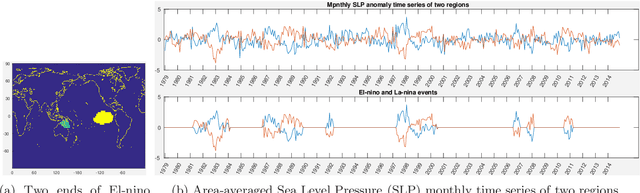
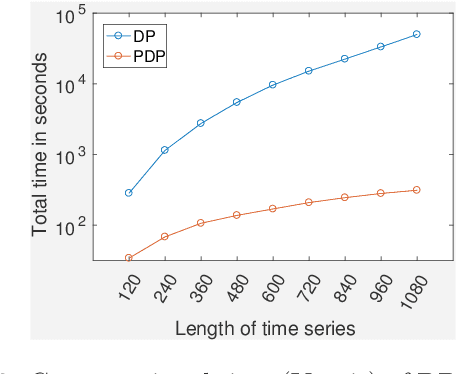
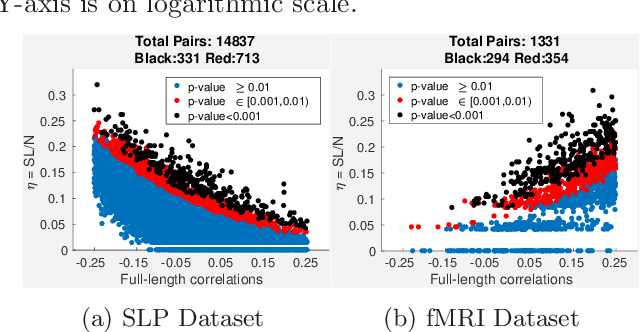

Abstract:Time-series data is being increasingly collected and stud- ied in several areas such as neuroscience, climate science, transportation, and social media. Discovery of complex patterns of relationships between individual time-series, using data-driven approaches can improve our understanding of real-world systems. While traditional approaches typically study relationships between two entire time series, many interesting relationships in real-world applications exist in small sub-intervals of time while remaining absent or feeble during other sub-intervals. In this paper, we define the notion of a sub-interval relationship (SIR) to capture inter- actions between two time series that are prominent only in certain sub-intervals of time. We propose a novel and efficient approach to find most interesting SIR in a pair of time series. We evaluate our proposed approach on two real-world datasets from climate science and neuroscience domain and demonstrated the scalability and computational efficiency of our proposed approach. We further evaluated our discovered SIRs based on a randomization based procedure. Our results indicated the existence of several such relationships that are statistically significant, some of which were also found to have physical interpretation.
Spatio-Temporal Data Mining: A Survey of Problems and Methods
Nov 17, 2017



Abstract:Large volumes of spatio-temporal data are increasingly collected and studied in diverse domains including, climate science, social sciences, neuroscience, epidemiology, transportation, mobile health, and Earth sciences. Spatio-temporal data differs from relational data for which computational approaches are developed in the data mining community for multiple decades, in that both spatial and temporal attributes are available in addition to the actual measurements/attributes. The presence of these attributes introduces additional challenges that needs to be dealt with. Approaches for mining spatio-temporal data have been studied for over a decade in the data mining community. In this article we present a broad survey of this relatively young field of spatio-temporal data mining. We discuss different types of spatio-temporal data and the relevant data mining questions that arise in the context of analyzing each of these datasets. Based on the nature of the data mining problem studied, we classify literature on spatio-temporal data mining into six major categories: clustering, predictive learning, change detection, frequent pattern mining, anomaly detection, and relationship mining. We discuss the various forms of spatio-temporal data mining problems in each of these categories.
Theory-guided Data Science: A New Paradigm for Scientific Discovery from Data
Nov 13, 2017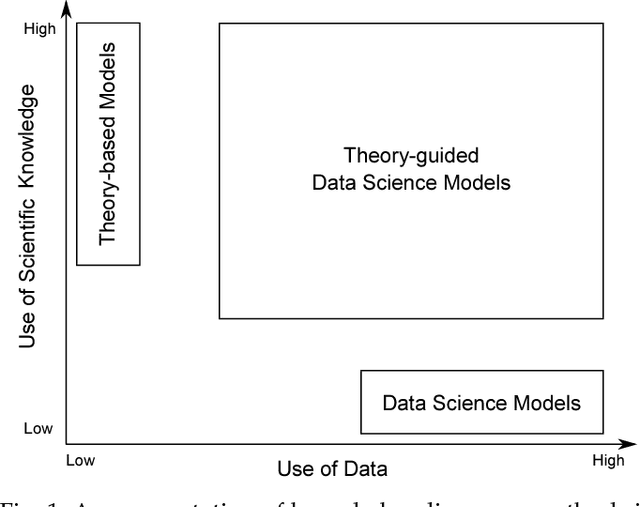

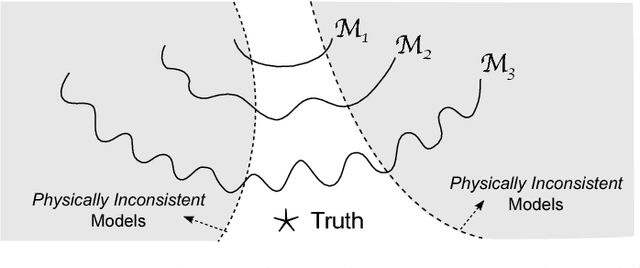
Abstract:Data science models, although successful in a number of commercial domains, have had limited applicability in scientific problems involving complex physical phenomena. Theory-guided data science (TGDS) is an emerging paradigm that aims to leverage the wealth of scientific knowledge for improving the effectiveness of data science models in enabling scientific discovery. The overarching vision of TGDS is to introduce scientific consistency as an essential component for learning generalizable models. Further, by producing scientifically interpretable models, TGDS aims to advance our scientific understanding by discovering novel domain insights. Indeed, the paradigm of TGDS has started to gain prominence in a number of scientific disciplines such as turbulence modeling, material discovery, quantum chemistry, bio-medical science, bio-marker discovery, climate science, and hydrology. In this paper, we formally conceptualize the paradigm of TGDS and present a taxonomy of research themes in TGDS. We describe several approaches for integrating domain knowledge in different research themes using illustrative examples from different disciplines. We also highlight some of the promising avenues of novel research for realizing the full potential of theory-guided data science.
Enhancing the functional content of protein interaction networks
Oct 25, 2012



Abstract:Protein interaction networks are a promising type of data for studying complex biological systems. However, despite the rich information embedded in these networks, they face important data quality challenges of noise and incompleteness that adversely affect the results obtained from their analysis. Here, we explore the use of the concept of common neighborhood similarity (CNS), which is a form of local structure in networks, to address these issues. Although several CNS measures have been proposed in the literature, an understanding of their relative efficacies for the analysis of interaction networks has been lacking. We follow the framework of graph transformation to convert the given interaction network into a transformed network corresponding to a variety of CNS measures evaluated. The effectiveness of each measure is then estimated by comparing the quality of protein function predictions obtained from its corresponding transformed network with those from the original network. Using a large set of S. cerevisiae interactions, and a set of 136 GO terms, we find that several of the transformed networks produce more accurate predictions than those obtained from the original network. In particular, the $HC.cont$ measure proposed here performs particularly well for this task. Further investigation reveals that the two major factors contributing to this improvement are the abilities of CNS measures, especially $HC.cont$, to prune out noisy edges and introduce new links between functionally related proteins.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge