High-Fidelity Diffusion Face Swapping with ID-Constrained Facial Conditioning

Face swapping aims to seamlessly transfer a source facial identity onto a target while preserving target attributes such as pose and expression. Diffusion models, known for their superior generative capabilities, have recently shown promise in advancing face-swapping quality. This paper addresses two key challenges in diffusion-based face swapping: the prioritized preservation of identity over target attributes and the inherent conflict between identity and attribute conditioning. To tackle these issues, we introduce an identity-constrained attribute-tuning framework for face swapping that first ensures identity preservation and then fine-tunes for attribute alignment, achieved through a decoupled condition injection. We further enhance fidelity by incorporating identity and adversarial losses in a post-training refinement stage. Our proposed identity-constrained diffusion-based face-swapping model outperforms existing methods in both qualitative and quantitative evaluations, demonstrating superior identity similarity and attribute consistency, achieving a new state-of-the-art performance in high-fidelity face swapping.

VividFace: A Diffusion-Based Hybrid Framework for High-Fidelity Video Face Swapping

Video face swapping is becoming increasingly popular across various applications, yet existing methods primarily focus on static images and struggle with video face swapping because of temporal consistency and complex scenarios. In this paper, we present the first diffusion-based framework specifically designed for video face swapping. Our approach introduces a novel image-video hybrid training framework that leverages both abundant static image data and temporal video sequences, addressing the inherent limitations of video-only training. The framework incorporates a specially designed diffusion model coupled with a VidFaceVAE that effectively processes both types of data to better maintain temporal coherence of the generated videos. To further disentangle identity and pose features, we construct the Attribute-Identity Disentanglement Triplet (AIDT) Dataset, where each triplet has three face images, with two images sharing the same pose and two sharing the same identity. Enhanced with a comprehensive occlusion augmentation, this dataset also improves robustness against occlusions. Additionally, we integrate 3D reconstruction techniques as input conditioning to our network for handling large pose variations. Extensive experiments demonstrate that our framework achieves superior performance in identity preservation, temporal consistency, and visual quality compared to existing methods, while requiring fewer inference steps. Our approach effectively mitigates key challenges in video face swapping, including temporal flickering, identity preservation, and robustness to occlusions and pose variations.

Escaping the Gradient Vanishing: Periodic Alternatives of Softmax in Attention Mechanism

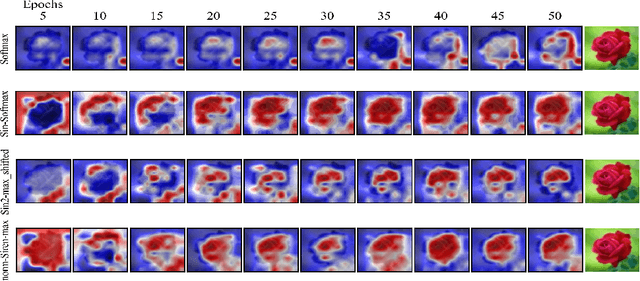
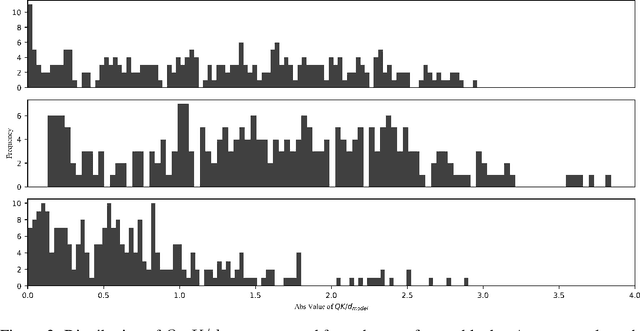
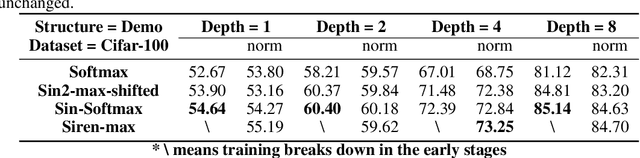
Softmax is widely used in neural networks for multiclass classification, gate structure and attention mechanisms. The statistical assumption that the input is normal distributed supports the gradient stability of Softmax. However, when used in attention mechanisms such as transformers, since the correlation scores between embeddings are often not normally distributed, the gradient vanishing problem appears, and we prove this point through experimental confirmation. In this work, we suggest that replacing the exponential function by periodic functions, and we delve into some potential periodic alternatives of Softmax from the view of value and gradient. Through experiments on a simply designed demo referenced to LeViT, our method is proved to be able to alleviate the gradient problem and yield substantial improvements compared to Softmax and its variants. Further, we analyze the impact of pre-normalization for Softmax and our methods through mathematics and experiments. Lastly, we increase the depth of the demo and prove the applicability of our method in deep structures.