Accelerated Fuzzy C-Means Clustering Based on New Affinity Filtering and Membership Scaling

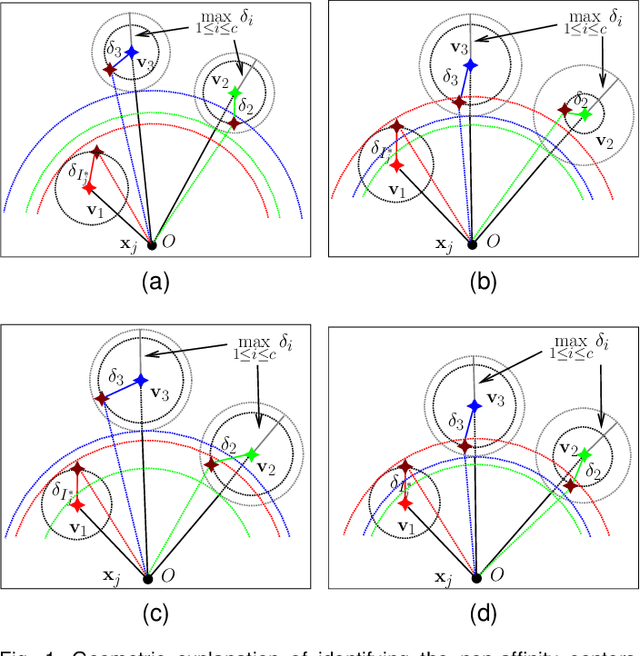
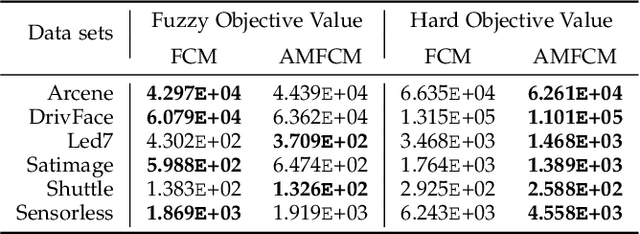
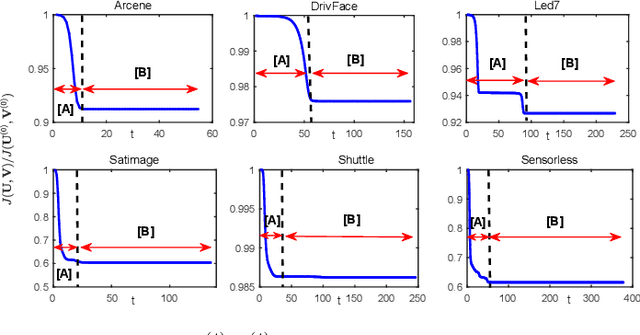
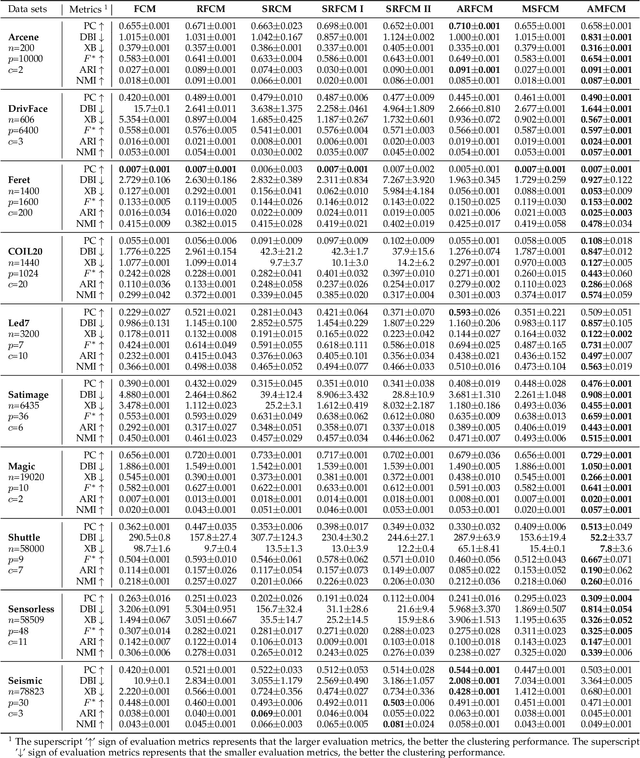
Fuzzy C-Means (FCM) is a widely used clustering method. However, FCM and its many accelerated variants have low efficiency in the mid-to-late stage of the clustering process. In this stage, all samples are involved in the update of their non-affinity centers, and the fuzzy membership grades of the most of samples, whose assignment is unchanged, are still updated by calculating the samples-centers distances. All those lead to the algorithms converging slowly. In this paper, a new affinity filtering technique is developed to recognize a complete set of the non-affinity centers for each sample with low computations. Then, a new membership scaling technique is suggested to set the membership grades between each sample and its non-affinity centers to 0 and maintain the fuzzy membership grades for others. By integrating those two techniques, FCM based on new affinity filtering and membership scaling (AMFCM) is proposed to accelerate the whole convergence process of FCM. Many experimental results performed on synthetic and real-world data sets have shown the feasibility and efficiency of the proposed algorithm. Compared with the state-of-the-art algorithms, AMFCM is significantly faster and more effective. For example, AMFCM reduces the number of the iteration of FCM by 80% on average.

Multi-Prototypes Convex Merging Based K-Means Clustering Algorithm

K-Means algorithm is a popular clustering method. However, it has two limitations: 1) it gets stuck easily in spurious local minima, and 2) the number of clusters k has to be given a priori. To solve these two issues, a multi-prototypes convex merging based K-Means clustering algorithm (MCKM) is presented. First, based on the structure of the spurious local minima of the K-Means problem, a multi-prototypes sampling (MPS) is designed to select the appropriate number of multi-prototypes for data with arbitrary shapes. A theoretical proof is given to guarantee that the multi-prototypes selected by MPS can achieve a constant factor approximation to the optimal cost of the K-Means problem. Then, a merging technique, called convex merging (CM), merges the multi-prototypes to get a better local minima without k being given a priori. Specifically, CM can obtain the optimal merging and estimate the correct k. By integrating these two techniques with K-Means algorithm, the proposed MCKM is an efficient and explainable clustering algorithm for escaping the undesirable local minima of K-Means problem without given k first. Experimental results performed on synthetic and real-world data sets have verified the effectiveness of the proposed algorithm.

Fast Kernel k-means Clustering Using Incomplete Cholesky Factorization

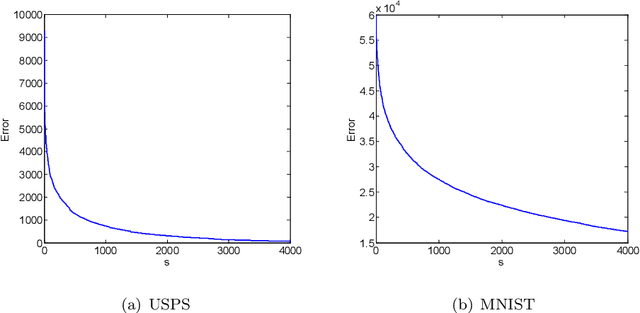
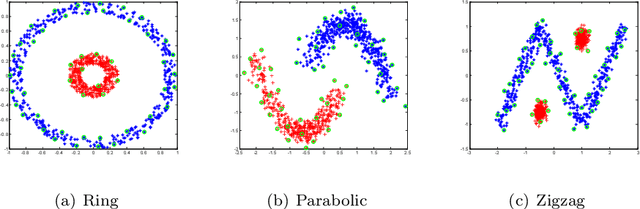
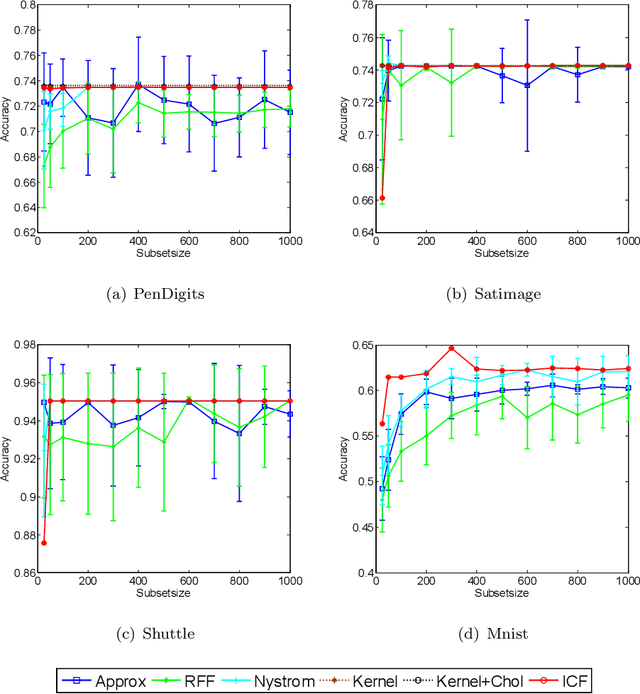
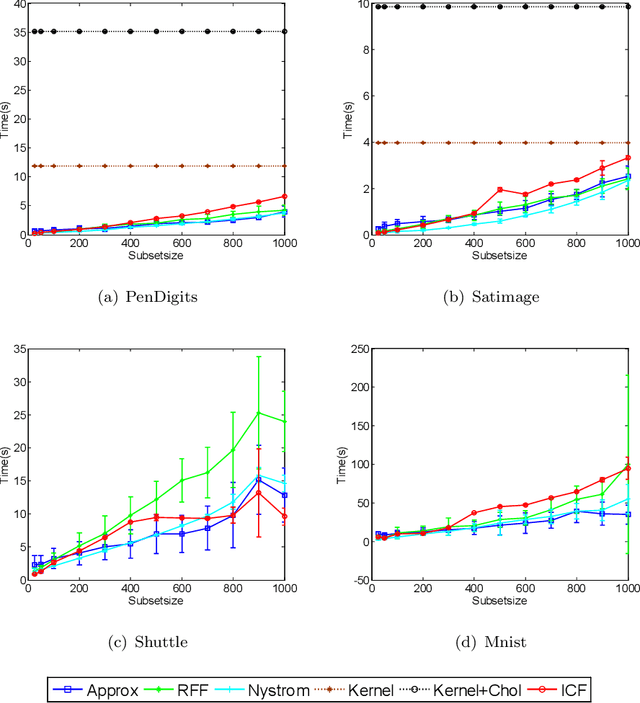
Kernel-based clustering algorithm can identify and capture the non-linear structure in datasets, and thereby it can achieve better performance than linear clustering. However, computing and storing the entire kernel matrix occupy so large memory that it is difficult for kernel-based clustering to deal with large-scale datasets. In this paper, we employ incomplete Cholesky factorization to accelerate kernel clustering and save memory space. The key idea of the proposed kernel $k$-means clustering using incomplete Cholesky factorization is that we approximate the entire kernel matrix by the product of a low-rank matrix and its transposition. Then linear $k$-means clustering is applied to columns of the transpose of the low-rank matrix. We show both analytically and empirically that the performance of the proposed algorithm is similar to that of the kernel $k$-means clustering algorithm, but our method can deal with large-scale datasets.

Stochastic Variance Reduction Gradient for a Non-convex Problem Using Graduated Optimization

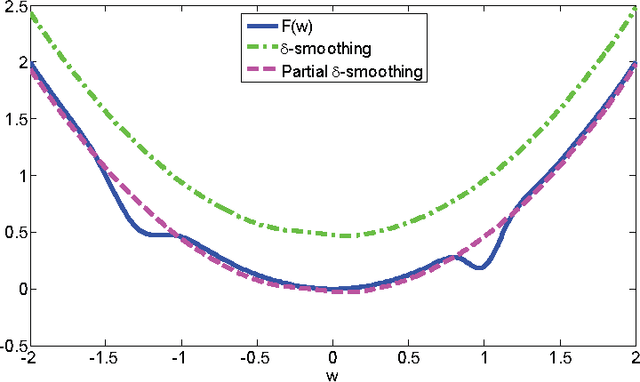
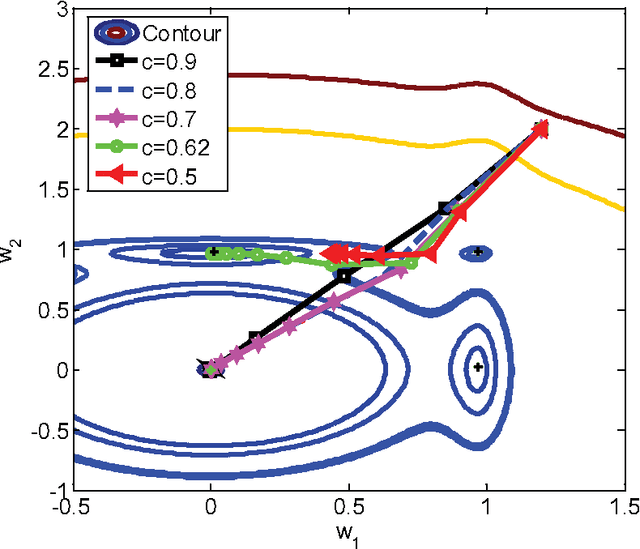
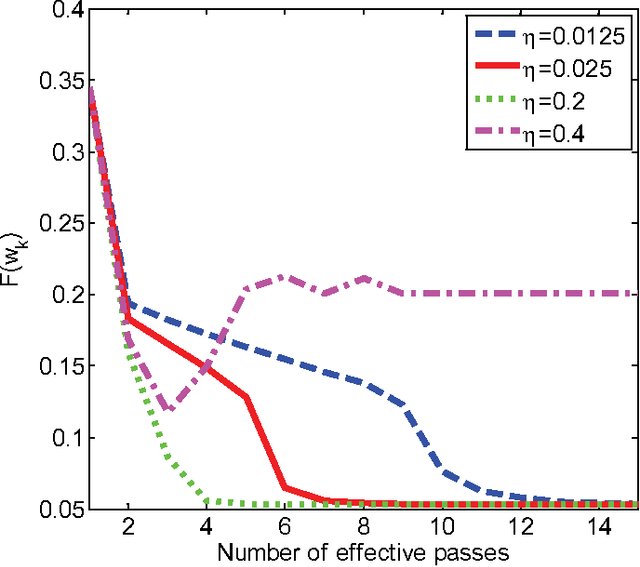
In machine learning, nonconvex optimization problems with multiple local optimums are often encountered. Graduated Optimization Algorithm (GOA) is a popular heuristic method to obtain global optimums of nonconvex problems through progressively minimizing a series of convex approximations to the nonconvex problems more and more accurate. Recently, such an algorithm GradOpt based on GOA is proposed with amazing theoretical and experimental results, but it mainly studies the problem which consists of one nonconvex part. This paper aims to find the global solution of a nonconvex objective with a convex part plus a nonconvex part based on GOA. By graduating approximating non-convex part of the problem and minimizing them with the Stochastic Variance Reduced Gradient (SVRG) or proximal SVRG, two new algorithms, SVRG-GOA and PSVRG-GOA, are proposed. We prove that the new algorithms have lower iteration complexity ($O(1/\varepsilon)$) than GradOpt ($O(1/\varepsilon^2)$). Some tricks, such as enlarging shrink factor, using project step, stochastic gradient, and mini-batch skills, are also given to accelerate the convergence speed of the proposed algorithms. Experimental results illustrate that the new algorithms with the similar performance can converge to 'global' optimums of the nonconvex problems, and they converge faster than the GradOpt and the nonconvex proximal SVRG.

Sparse Algorithm for Robust LSSVM in Primal Space

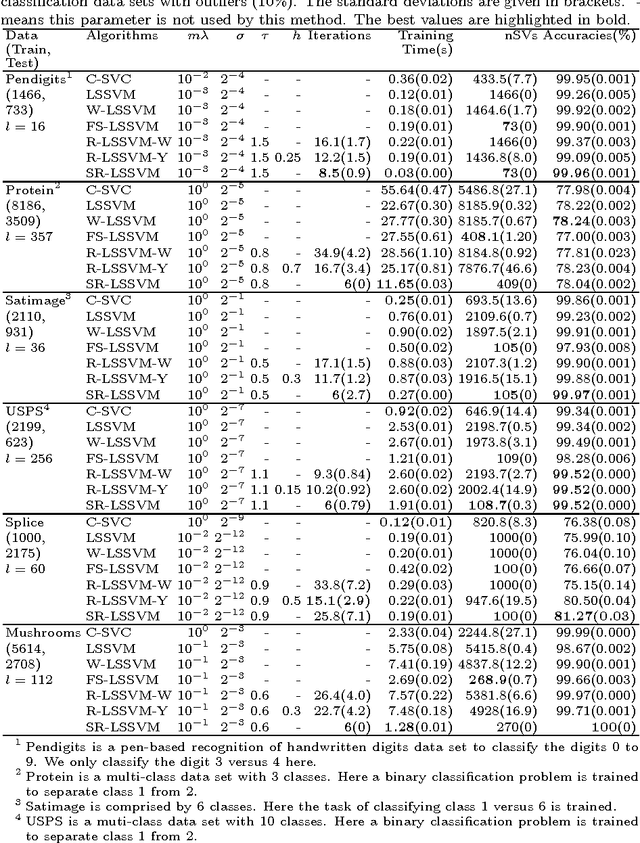
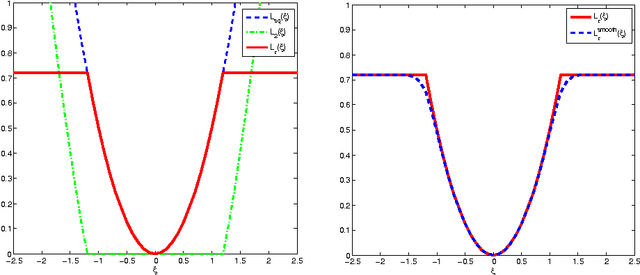
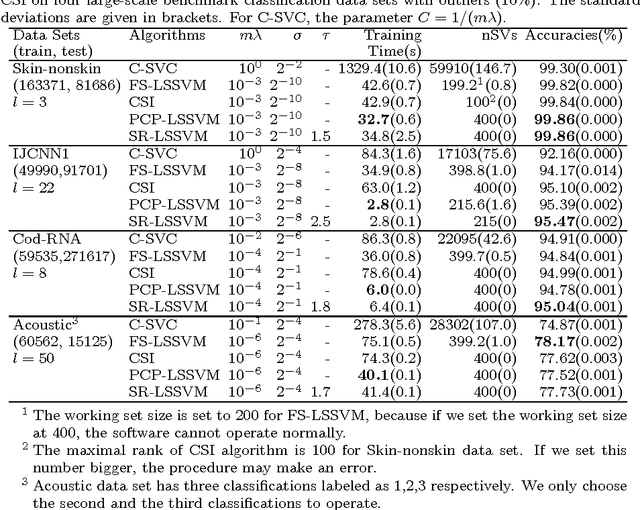
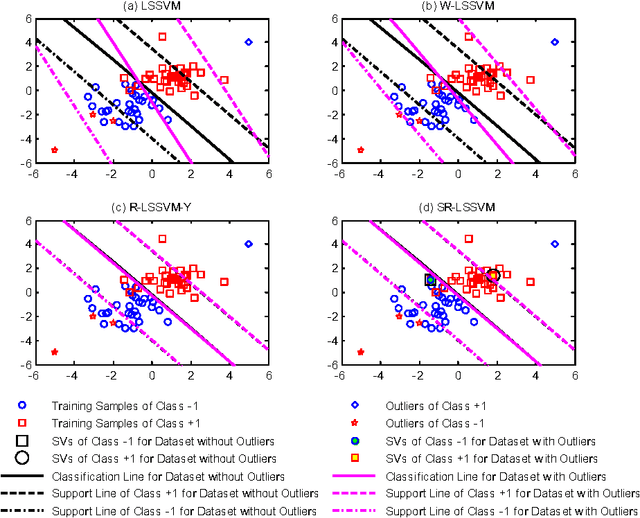
As enjoying the closed form solution, least squares support vector machine (LSSVM) has been widely used for classification and regression problems having the comparable performance with other types of SVMs. However, LSSVM has two drawbacks: sensitive to outliers and lacking sparseness. Robust LSSVM (R-LSSVM) overcomes the first partly via nonconvex truncated loss function, but the current algorithms for R-LSSVM with the dense solution are faced with the second drawback and are inefficient for training large-scale problems. In this paper, we interpret the robustness of R-LSSVM from a re-weighted viewpoint and give a primal R-LSSVM by the representer theorem. The new model may have sparse solution if the corresponding kernel matrix has low rank. Then approximating the kernel matrix by a low-rank matrix and smoothing the loss function by entropy penalty function, we propose a convergent sparse R-LSSVM (SR-LSSVM) algorithm to achieve the sparse solution of primal R-LSSVM, which overcomes two drawbacks of LSSVM simultaneously. The proposed algorithm has lower complexity than the existing algorithms and is very efficient for training large-scale problems. Many experimental results illustrate that SR-LSSVM can achieve better or comparable performance with less training time than related algorithms, especially for training large scale problems.