Using Multilevel Circulant Matrix Approximate to Speed Up Kernel Logistic Regression

Kernel logistic regression (KLR) is a classical nonlinear classifier in statistical machine learning. Newton method with quadratic convergence rate can solve KLR problem more effectively than the gradient method. However, an obvious limitation of Newton method for training large-scale problems is the $O(n^{3})$ time complexity and $O(n^{2})$ space complexity, where $n$ is the number of training instances. In this paper, we employ the multilevel circulant matrix (MCM) approximate kernel matrix to save in storage space and accelerate the solution of the KLR. Combined with the characteristics of MCM and our ingenious design, we propose an MCM approximate Newton iterative method. We first simplify the Newton direction according to the semi-positivity of the kernel matrix and then perform a two-step approximation of the Newton direction by using MCM. Our method reduces the time complexity of each iteration to $O(n \log n)$ by using the multidimensional fast Fourier transform (mFFT). In addition, the space complexity can be reduced to $O(n)$ due to the built-in periodicity of MCM. Experimental results on some large-scale binary and multi-classification problems show that our method makes KLR scalable for large-scale problems, with less memory consumption, and converges to test accuracy without sacrifice in a shorter time.

Stochastic Variance Reduction Gradient for a Non-convex Problem Using Graduated Optimization

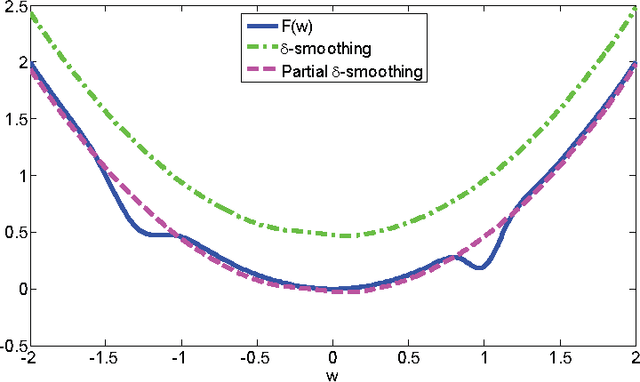
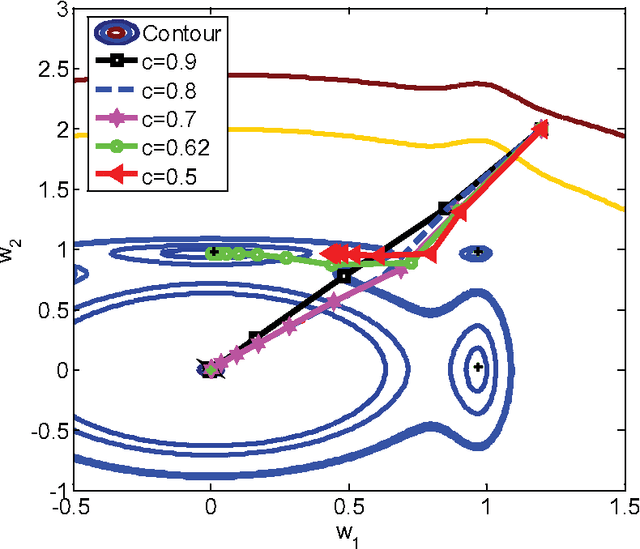
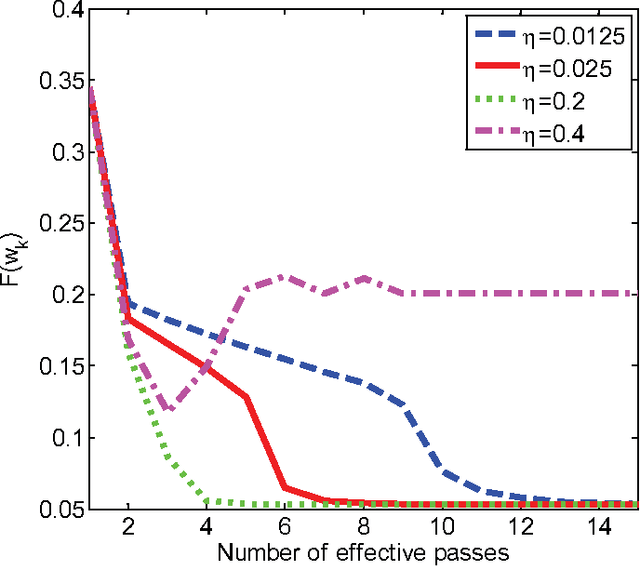
In machine learning, nonconvex optimization problems with multiple local optimums are often encountered. Graduated Optimization Algorithm (GOA) is a popular heuristic method to obtain global optimums of nonconvex problems through progressively minimizing a series of convex approximations to the nonconvex problems more and more accurate. Recently, such an algorithm GradOpt based on GOA is proposed with amazing theoretical and experimental results, but it mainly studies the problem which consists of one nonconvex part. This paper aims to find the global solution of a nonconvex objective with a convex part plus a nonconvex part based on GOA. By graduating approximating non-convex part of the problem and minimizing them with the Stochastic Variance Reduced Gradient (SVRG) or proximal SVRG, two new algorithms, SVRG-GOA and PSVRG-GOA, are proposed. We prove that the new algorithms have lower iteration complexity ($O(1/\varepsilon)$) than GradOpt ($O(1/\varepsilon^2)$). Some tricks, such as enlarging shrink factor, using project step, stochastic gradient, and mini-batch skills, are also given to accelerate the convergence speed of the proposed algorithms. Experimental results illustrate that the new algorithms with the similar performance can converge to 'global' optimums of the nonconvex problems, and they converge faster than the GradOpt and the nonconvex proximal SVRG.