Fast Kernel k-means Clustering Using Incomplete Cholesky Factorization
Paper and Code
Feb 07, 2020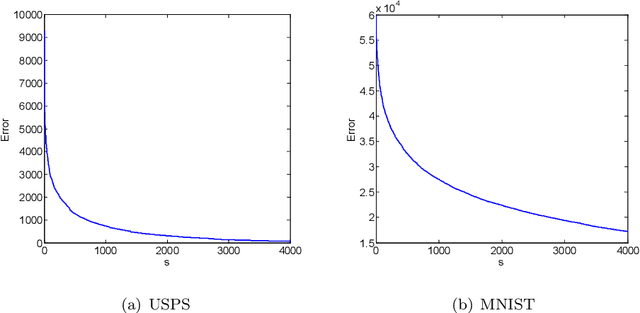
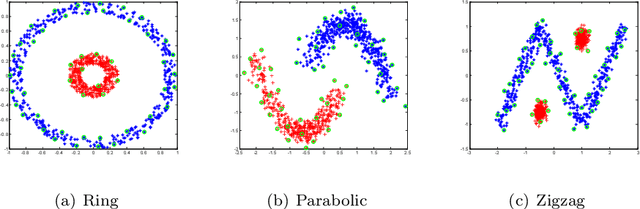
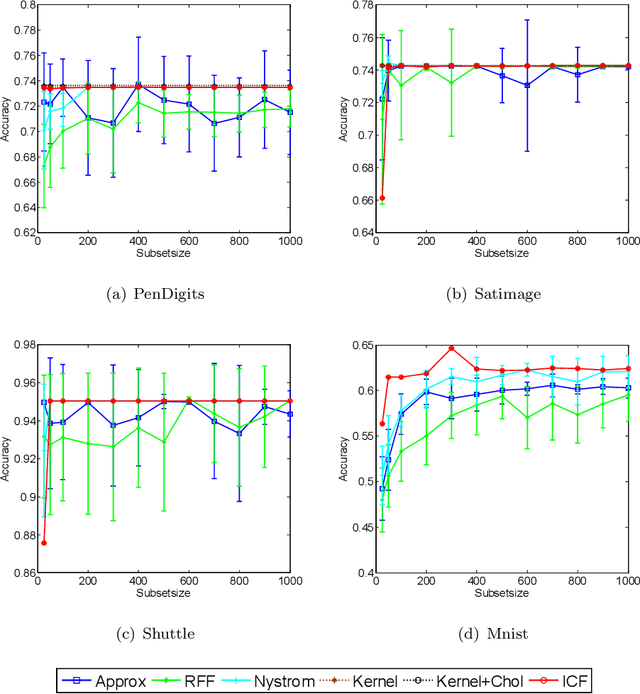
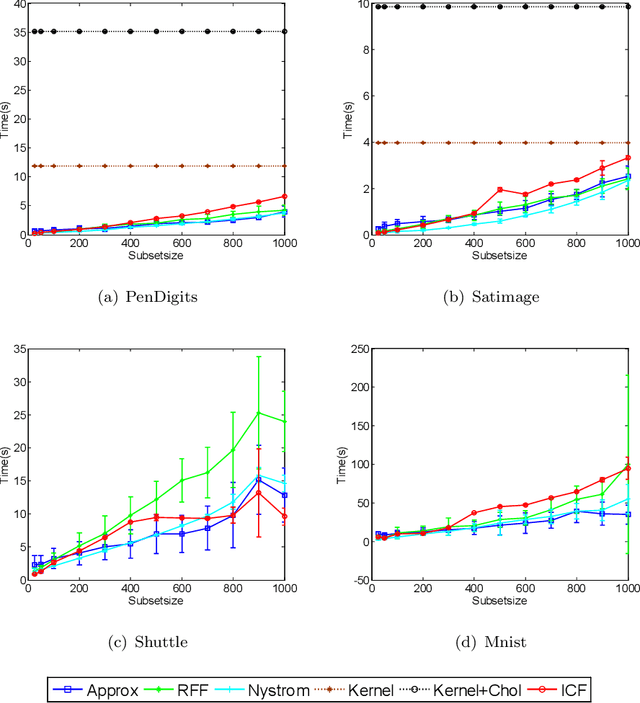
Kernel-based clustering algorithm can identify and capture the non-linear structure in datasets, and thereby it can achieve better performance than linear clustering. However, computing and storing the entire kernel matrix occupy so large memory that it is difficult for kernel-based clustering to deal with large-scale datasets. In this paper, we employ incomplete Cholesky factorization to accelerate kernel clustering and save memory space. The key idea of the proposed kernel $k$-means clustering using incomplete Cholesky factorization is that we approximate the entire kernel matrix by the product of a low-rank matrix and its transposition. Then linear $k$-means clustering is applied to columns of the transpose of the low-rank matrix. We show both analytically and empirically that the performance of the proposed algorithm is similar to that of the kernel $k$-means clustering algorithm, but our method can deal with large-scale datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge