Sparse Algorithm for Robust LSSVM in Primal Space
Paper and Code
Feb 07, 2017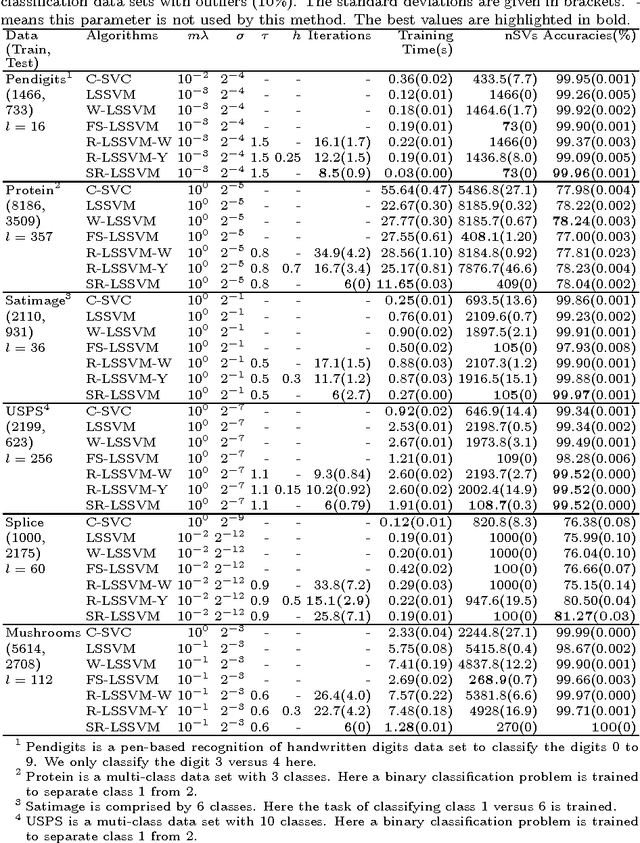
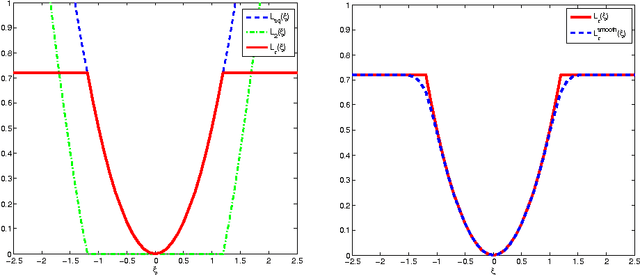
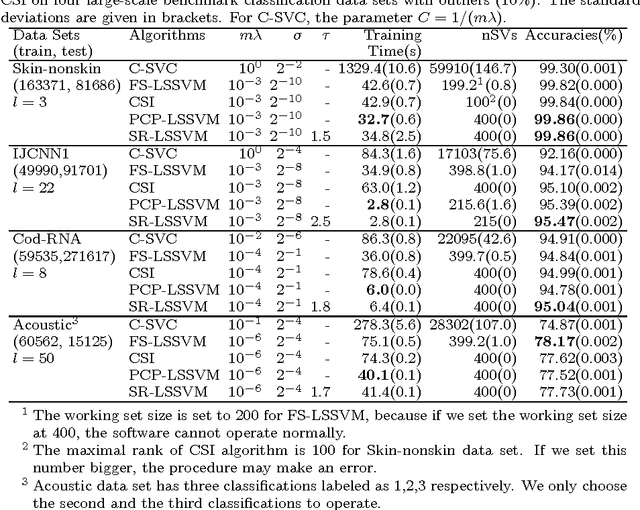
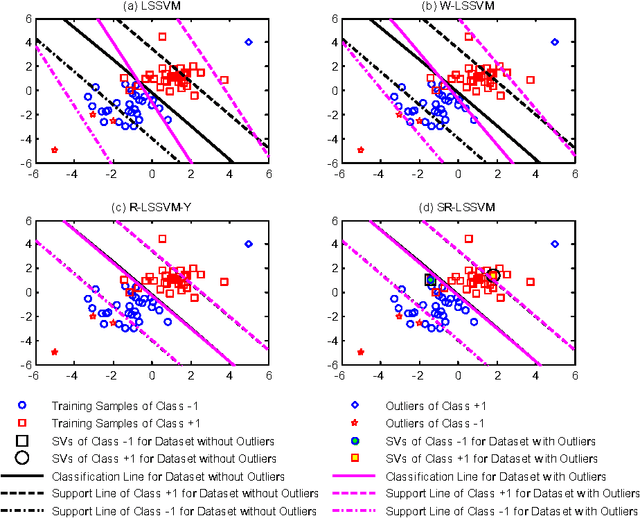
As enjoying the closed form solution, least squares support vector machine (LSSVM) has been widely used for classification and regression problems having the comparable performance with other types of SVMs. However, LSSVM has two drawbacks: sensitive to outliers and lacking sparseness. Robust LSSVM (R-LSSVM) overcomes the first partly via nonconvex truncated loss function, but the current algorithms for R-LSSVM with the dense solution are faced with the second drawback and are inefficient for training large-scale problems. In this paper, we interpret the robustness of R-LSSVM from a re-weighted viewpoint and give a primal R-LSSVM by the representer theorem. The new model may have sparse solution if the corresponding kernel matrix has low rank. Then approximating the kernel matrix by a low-rank matrix and smoothing the loss function by entropy penalty function, we propose a convergent sparse R-LSSVM (SR-LSSVM) algorithm to achieve the sparse solution of primal R-LSSVM, which overcomes two drawbacks of LSSVM simultaneously. The proposed algorithm has lower complexity than the existing algorithms and is very efficient for training large-scale problems. Many experimental results illustrate that SR-LSSVM can achieve better or comparable performance with less training time than related algorithms, especially for training large scale problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge